Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

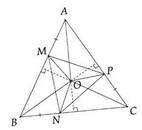
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP

Tự vẽ hình nha ^^
a, Ta có: tam giác ABC cân tại A có AO là đường trung trực (gt)
=> AO cũng là phân giác của góc BAC
=> góc OAB = góc OAC (1)
Gọi OD là đường trung trực của AC
Xét tam giác AOC có OD vừa là đường cao vừa là trung tuyến => AOC cân tại O
=> góc OAC = góc OCA (2)
Từ (1), (2) => đpcm
b, Theo câu a: tam giác AOC cân tại O
=> OA = OC (3)
Và MA = CN (gt) (4)
Mặt khác: góc MAC = góc ABC + góc ACB (góc ngoài)
=> góc MAO = góc MAC + góc OAC = góc ABC + góc ACB + góc OAC (*)
Góc BCN = góc BAC + góc ABC (góc ngoài)
=> góc OCN = góc BCN + góc OCB = góc BAC + góc ABC + góc ACB - góc OCA
<=> góc OCN = góc ABC + góc ACB + (góc BAC - góc OAB) (góc OAB = góc OCA théo câu a)
<=> góc OCN = góc ABC + góc ACB + góc OAC (**)
Từ (*), (**) => góc MAO = góc OCN (5)
Từ (3), (4), (5) => tam giác OAM = tam giác OCN (c-g-c)

bài 2:
ta có : điểm M nằm trên đường trung trực của BC nên M sẽ cách đều B và C => MB=MC
Ta có: AC=AM+MC
=> AC=AM+MB
Bài 2: Tam giác BNC cân tại N vì đường thẳng hạ từ N xuống vuong góc cạnh đối diện cũng là trung tuyến nên BN=NC
=> AN+BN=AN+NC=AC

đm con mặt lồn
im đi Lê Minh Phương