
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(P=\left(\dfrac{2x}{x+3}+\dfrac{x}{x-3}-\dfrac{3x^2+3}{x^2-9}\right):\left(\dfrac{2x-2}{x-3}-1\right)\)
\(\Rightarrow P=\dfrac{2x\left(x-3\right)+x\left(x+3\right)-\left(3x^2+3\right)}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x-2-\left(x-3\right)}{x-3}\)
\(\Rightarrow P=\dfrac{2x^2-6x+x^2+3x-3x^2-3}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x-2-x+3}{x-3}\)
\(\Rightarrow P=\dfrac{-3x-3}{\left(x+3\right)\left(x-3\right)}:\dfrac{x+1}{x-3}\)
\(\Rightarrow P=\dfrac{-3\left(x+1\right)}{\left(x+3\right)\left(x-3\right)}.\dfrac{x-3}{x+1}\)
\(\Rightarrow P=\dfrac{-3}{x+3}\)




a. \(D=\left(\dfrac{x^2-3x}{x^2-9}-1\right):\left(\dfrac{9-x^2}{x^2+x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right)\)
\(=\left[\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-1\right]:\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x^2-2x+3x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-1\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x\left(x-2\right)+3\left(x-2\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-\dfrac{x+3}{x+3}\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{\left(x-2\right)\left(x+3\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\dfrac{3}{x+3}:\left(\dfrac{3-x}{x-2}-\dfrac{3-x}{x-2}-\dfrac{x-2}{x+3}\right)\)
\(=\dfrac{3}{x+3}:\dfrac{x-2}{x+3}\)
\(=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{3}{x-2}\)

\(56^2+44^2+2.44.56\)
\(=\left(56+44\right)^2\)
\(=100^2=10000\)

Bài 2:
a: Xét ΔABC có
X là trung điểm của BC
Y là trung điểm của AB
Do đó: XY là đường trung bình
=>XY//AC và XY=AC/2=3,5(cm)
hay XZ//AC và XZ=AC
b: Xét tứ giác AZBX có
Y là trung điểm của AB
Y là trung điểm của ZX
Do đó: AZBX là hình bình hành
mà \(\widehat{AXB}=90^0\)
nên AZBX là hình chữ nhật
d: Xét tứ giác AZXC có
XZ//AC
XZ=AC
Do đó: AZXC là hình bình hành

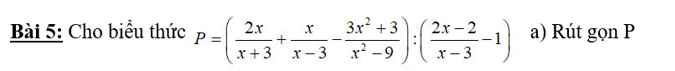


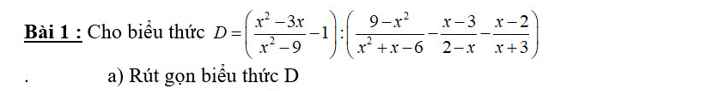

Bài 2:
b: =>(x-5)(x+3)=0
hay x=5 hoặc x=-3