K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 7 2019
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
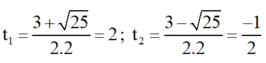
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
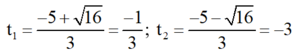
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
T
1
SA
14 tháng 6 2021
\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4
A
, mình đang cần giải gấp. Cảm ơn mn nhiều.
1
3 tháng 9 2021
Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)
A
0
A
1
26 tháng 9 2021
c: \(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+m\left(5-2\sqrt{3}\right)+2=\sqrt{2-1}+2m+2\)
\(\Leftrightarrow\sqrt{3}+1+m\left(5-2\sqrt{3}\right)=2m+3\)
\(\Leftrightarrow m\left(3-2\sqrt{3}\right)=2-\sqrt{3}\)
hay \(m=-\dfrac{\sqrt{3}}{3}\)
TT
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
a.
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=x+1\)
Pt trở thành:
\(a+b=2\left(a^2-b^2\right)\)
\(\Leftrightarrow a+b=\left(2a-2b\right)\left(a+b\right)\)
\(\Leftrightarrow2a-2b=1\) (do \(a+b>0\))
\(\Leftrightarrow2a=2b+1\)
\(\Leftrightarrow2\sqrt{x^2+2x+3}=2\sqrt{x^2+x+2}+1\)
\(\Leftrightarrow4\left(x^2+2x+3\right)=4\left(x^2+x+2\right)+1+4\sqrt{x^2+x+2}\)
\(\Leftrightarrow4x+3=4\sqrt{x^2+x+2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\16\left(x^2+x+2\right)=\left(4x+3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\8x=23\end{matrix}\right.\) \(\Rightarrow x=\dfrac{23}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
b.
ĐKXĐ: \(x\ge3\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x-3}=a\ge0\\\sqrt{x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=-5\)
Phương trình trở thành:
\(\left(a-b\right)\left(ab+1\right)=a^2-b^2\)
\(\Leftrightarrow\left(a-b\right)\left(ab+1\right)=\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\left(vô-nghiệm\right)\\ab+1=a+b\end{matrix}\right.\)
\(\Rightarrow ab-a-b+1=0\)
\(\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=1\\\sqrt{x+2}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1\left(ktm\right)\end{matrix}\right.\)
10 tháng 6 2021
1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)
PA
1
17 tháng 7 2021
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
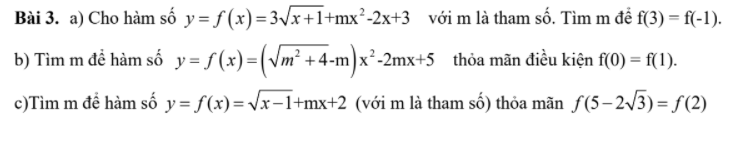
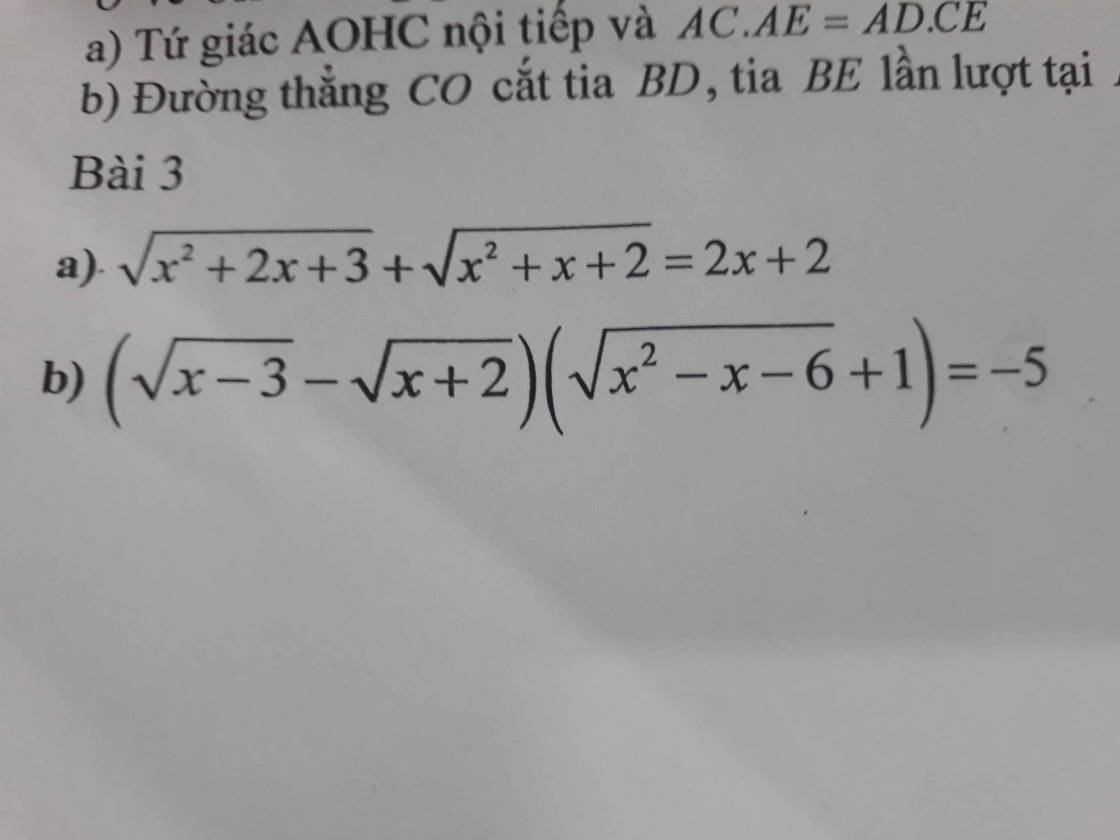
\(4x-9.3x-10.2x=0\)
\(=>4x-27x-20x=0\)
\(=>x\left(4-27-20\right)=0\)
\(=>x.\left(-43\right)=0\)
\(=>x=0\)