
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\)
\(b,\)Để có hệ số góc bằng 3 thì \(m-1=3\Leftrightarrow m=4\)
\(2,\\ 1,\left\{{}\begin{matrix}x+4y=8\\2x+5y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+8y=16\\2x+5y=13\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+5y=13\\3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+5=13\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=1\end{matrix}\right.\\ 2,\\ a,B=\left[\dfrac{6}{a-1}+\dfrac{10-2\sqrt{a}}{\left(a-1\right)\left(\sqrt{a}-1\right)}\right]\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\\ B=\dfrac{6\sqrt{a}-6+10-2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)^2}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\\ B=\dfrac{4\sqrt{a}+4}{4\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{1}{\sqrt{a}}=\dfrac{\sqrt{a}}{a}\)
\(b,C=B\left(a-\sqrt{a}+1\right)=\dfrac{\sqrt{a}\left(a-\sqrt{a}+1\right)}{a}=\dfrac{a\sqrt{a}-a+\sqrt{a}}{a}\\ C=\sqrt{a}-1+\dfrac{1}{\sqrt{a}}\ge2\sqrt{\sqrt{a}\cdot\dfrac{1}{\sqrt{a}}}-1=2-1=1\\ C_{min}=1\Leftrightarrow\sqrt{a}=\dfrac{1}{\sqrt{a}}\Leftrightarrow a=1\)

Bài 1:
a: \(A=2\sqrt{3}-\sqrt{27}+\sqrt{4-2\sqrt{3}}\)
\(=2\sqrt{3}-3\sqrt{3}+\sqrt{3}-1\)
=-1

Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....


a) Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI (1)
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b (2)
Từ (1) và (2)
=> sinA/sinB = a/b => a/sinA = b/sinB
CMTT ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC

 Làm giúp mk ý c bài 5.5
Làm giúp mk ý c bài 5.5








5.5:
a: Vì (d)//y=1/2x-1 nên a=1/2
=>y=1/2x+b
Thay x=0 và y=2 vào (d), ta được;
b+1/2*0=2
=>b=2
=>(d): y=1/2x+2
b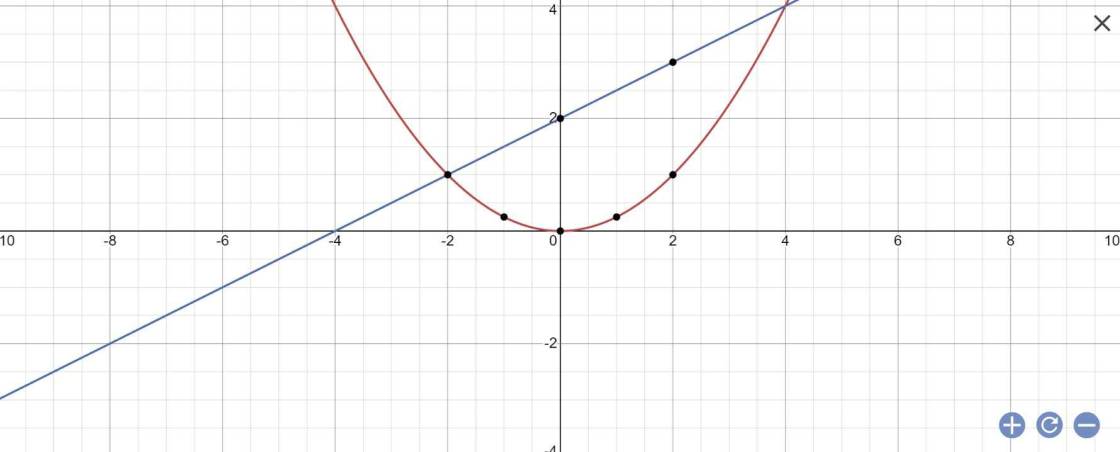
c: PTHDGĐ là:
1/4x^2=1/2x+2
=>1/4x^2-1/2x-2=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
Khi x=4 thì y=1/4*x^2=1/4*4^2=4
Khi x=-2 thì y=1/4*(-2)^2=1
=>A(4;4); B(-2;1)
\(OA=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(OB=\sqrt{\left(-2\right)^2+1^2}=\sqrt{5}\)
\(AB=\sqrt{\left(-2-4\right)^2+\left(1-4\right)^2}=3\sqrt{5}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=-\dfrac{\sqrt{10}}{10}\)
=>\(sinAOB=\dfrac{3\sqrt{10}}{10}\)
\(S_{OAB}=\dfrac{1}{2}\cdot4\sqrt{2}\cdot\sqrt{5}\cdot\dfrac{3}{\sqrt{10}}=2\cdot3=6\)
thanks