K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
H
2
13 tháng 3 2022
2) -Xét △OAE và △OBG có:
\(OA=OB\) (O là tâm của hình vuông ABCD)
\(AE=BG\left(gt\right)\)
\(OE=OG\) (△OGE vuông cân tại O)
\(\Rightarrow\)△OAE=△OBG (c-c-c).
\(\Rightarrow S_{OAE}=S_{OBG}\)
-Có: \(AE=BG\left(gt\right)\) ; \(AB=BC\) (ABCD là hình vuông)
\(\Rightarrow AB-AE=BC-BG\) nên \(BE=CG\)
-Xét △OBE và △OCG có:
\(OA=OB\) (O là tâm của hình vuông ABCD)
\(BE=CG\left(cmt\right)\)
\(OE=OG\) (△OGE vuông cân tại O)
\(\Rightarrow\)△OBE=△OCG (c-c-c).
\(\Rightarrow S_{OBE}=S_{OCG}\)
-Có: \(S_{OBE}+S_{OCG}+S_{OAE}+S_{OBG}=S_{ABC}\)
\(\Rightarrow S_{OBE}+S_{OBE}+S_{OBG}+S_{OBG}=\dfrac{S_{ABCD}}{2}=\dfrac{a^2}{2}\)
\(\Rightarrow2.\left(S_{OBE}+S_{OBG}\right)=\dfrac{a^2}{2}\)
\(\Rightarrow S_{OEBG}=\dfrac{a^2}{4}\)
13 tháng 3 2022
3) -Xét △CHG có: CH//AB (ABCD là hình vuông)
\(\Rightarrow\dfrac{AG}{HG}=\dfrac{BG}{CG}\) (định lí Ta-let)
Mà \(BG=AE\left(gt\right);CG=BE\left(cmt\right)\) nên \(\dfrac{AG}{HG}=\dfrac{AE}{BE}\)
-Xét △ABH có: \(\dfrac{AG}{HG}=\dfrac{AE}{BE}\) (cmt) nên EG//BH.
DL
1
15 tháng 11 2021
a: \(A=\left(x+2+2x-5\right)^2=\left(3x-3\right)^2\)
\(=\left(\dfrac{3}{4}-3\right)^2=\left(-\dfrac{9}{4}\right)^2=\dfrac{81}{16}\)
28 tháng 6 2023
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
4 tháng 5 2021
Em tách ra mỗi lần hỏi đăng 1-3 bài thôi để nhận hỗ trợ sớm nhất nha em!
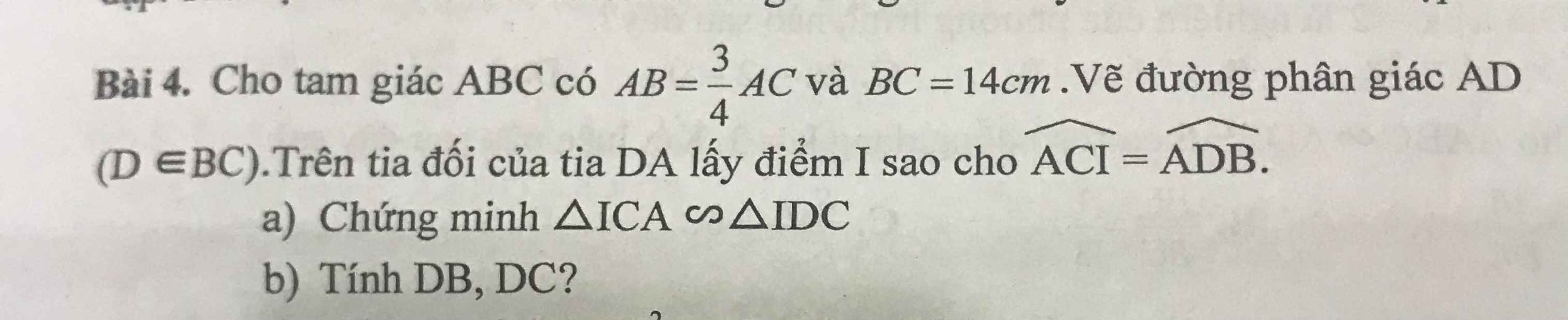
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: \(AM=\dfrac{AB}{2}\)
\(AN=\dfrac{AC}{2}\)
\(MN=\dfrac{BC}{2}\)
mà AB=AC=BC
nên AM=MN=AN
hay ΔAMN đều