
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{6}=\dfrac{a+b-c}{2+5-6}=60\)
Do đó: a=120; b=300; c=360

Bài 3:
a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)

\(M=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\)
+)Ta thấy:\(\frac{a}{b+c}>\frac{a}{a+b+c}\)
\(\frac{b}{a+c}>\frac{b}{a+b+c}\)
\(\frac{c}{a+b}>\frac{c}{a+b+c}\)
\(\Rightarrow M>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1\)
Vậy M>1 (1) (Đề sai )
b)\(M=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\)
+)Ta thấy:\(\frac{a}{b+c}< \frac{a+a}{a+b+c}=\frac{2a}{a+b+c}\)
\(\frac{b}{a+c}< \frac{b+b}{a+b+c}=\frac{2b}{a+b+c}\)
\(\frac{c}{a+b}< \frac{c+c}{a+b+c}=\frac{2c}{a+b+c}\)
\(\Rightarrow M< \frac{2a}{a+b+c}+\frac{2b}{a+b+c}+\frac{2c}{a+b+c}=\frac{2a+2b+2c}{a+b+c}=\frac{2.\left(a+b+c\right)}{a+b+c}=2\)
=>M<2 (2)
+)Từ (1) và (2)
=>M không phải là ssoos nguyên
Chúc bạn học tốt

a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
b: Xét ΔEAD có
EB là đường cao
EB là đường trung tuyếm
Do đó: ΔEAD cân tại E
b:

a: \(\widehat{B}>\widehat{C}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔBDC có HB<HC
mà HB là hình chiếu của BD trên BC
và HC là hình chiếu của CD trên BC
nên BD<CD
xét tam giác ABC có góc B lớn hơn góc C.
==> AB<AC (quan hệ giữa cạnh và góc đối diện trong 1 tamgiac)
Xét ΔABC ta có
AB<AC(cmt)
mà HC là hình chiếu của AC trên BC
HB là hình chiếu của AB trên BC
==> HB<HC
Xét ΔBDC ta có
HB<HC( c/m ở câu a)
mà HC là hình chiếu của CD trên BC
HB là hình chiếu của BD trên BC
===> BD<CD
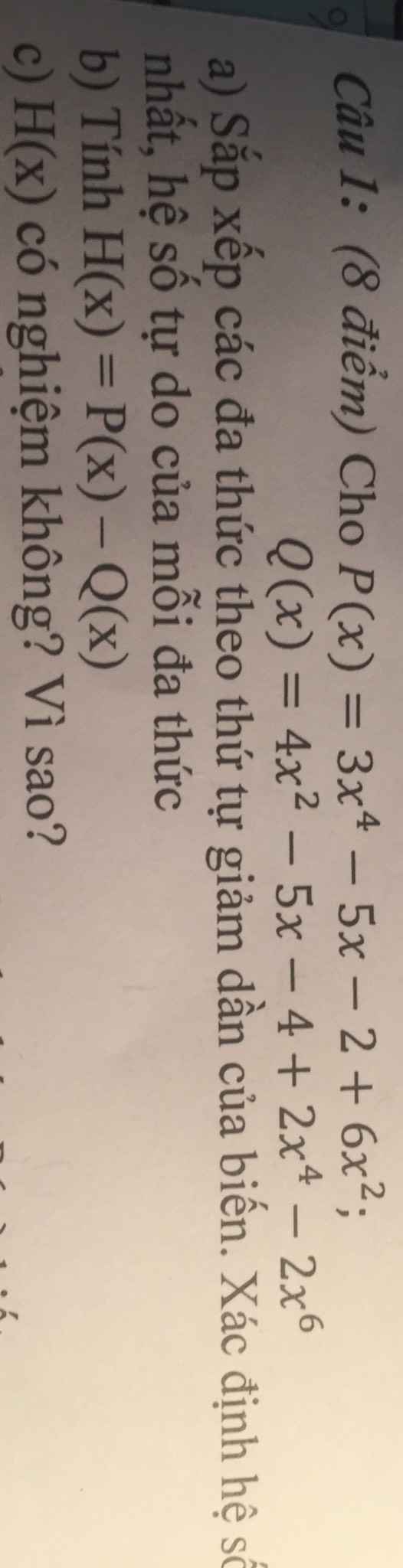

 Giúp mình làm câu này với
Giúp mình làm câu này với làm giúp mình câu 3và4 với ạ
làm giúp mình câu 3và4 với ạ
a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm