Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(0< \frac{a}{b}< 1\) nên ta có thể giả sử a và b là 2 số nguyên dương
Do đó ta có :
\(0< a< b\Rightarrow b-a>0\)
Ta có :
\(y-x=\frac{\left(b-a\right)c}{\left(b+c\right)b}>0\)
=> y > x ( đpcm)
Các bạn xem bài làm của mình , còn thiếu sót gì mong các bạn bỏ qua.
Sgk

c+d=a+b
a+d<c+b
\(\Rightarrow\)a+d+c+d<c+b+a+b
hay a+2d+c<c+2b+a
\(\Rightarrow\)2d<2b
\(\Rightarrow\)d<b(1)
lại có :c+b+c+d>a+d+a+b
\(\Rightarrow\)2c+b+d>2a+d+b
\(\Rightarrow\)2c>2a
\(\Rightarrow\)c>a(2)
từ(1)và(2)\(\Rightarrow\)Thứ tự giảm dần của a,b,c,d là: c,a,b,d(c>a>b>d)

\(\frac{a}{c}=\frac{c}{b}\Rightarrow c^2=ab\).
\(\frac{a^2+c^2}{b^2+c^2}=\frac{a^2+ab}{b^2+ab}=\frac{a\left(a+b\right)}{b\left(b+a\right)}=\frac{a}{b}\)
Ta có :
\(\frac{a}{c}=\frac{c}{b}\Rightarrow\frac{a^2}{c^2}=\frac{c^2}{b^2}=\frac{a^2+c^2}{c^2+b^2}\)
\(\frac{a}{b}=\frac{a}{c}.\frac{c}{b}=\left(\frac{a}{c}\right)^2\)
Mà \(\frac{a^2+c^2}{c^2+b^2}=\left(\frac{a}{c}\right)^2=\frac{a}{b}\). Vậy \(\frac{a^2+c^2}{b^2+c^2}=\frac{a}{b}\)

\(b^2=ac\Rightarrow\frac{a}{b}=\frac{b}{c}\) (1)
\(c^2=bd\Rightarrow\frac{b}{c}=\frac{c}{d}\) (2)
\(d^2=ce\Rightarrow\frac{c}{d}=\frac{d}{e}\) (3)
\(e^2=dg\Rightarrow\frac{d}{e}=\frac{e}{g}\) (4)
Từ (1),(2),(3),(4) suy ra \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{e}=\frac{e}{g}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{e}=\frac{e}{g}=\frac{a+b+c+d+e}{b+c+d+e+g}\)
Ta có: \(\frac{a}{b}=\frac{a+b+c+d+e}{b+c+d+e+g}\) (5)
\(\frac{b}{c}=\frac{a+b+c+d+e}{b+c+d+e+g}\) (6)
\(\frac{c}{d}=\frac{a+b+c+d+e}{b+c+d+e+g}\) (7)
\(\frac{d}{e}=\frac{a+b+c+d+e}{b+c+d+e+g}\) (8)
\(\frac{e}{g}=\frac{a+b+c+d+e}{b+c+d+e+g}\) (9)
Nhân (5),(6),(7),(8),(9) vế với vế:
\(\frac{a}{b}\cdot\frac{b}{c}\cdot\frac{c}{d}\cdot\frac{d}{e}\cdot\frac{e}{g}=\frac{a}{g}=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^5\) (đpcm)
P/s: Mk nghĩ đề là c/m: a/g = (a+b+c+d+e/b+c+d+e+g)^5

Áp dụng t/c dtsbn:
\(a+b+c=\dfrac{c}{a+b+1}=\dfrac{a}{b+c+2}=\dfrac{b}{a+c-3}=\dfrac{a+b+c}{2a+2b+2c}=\dfrac{1}{2}\\ \Rightarrow\left\{{}\begin{matrix}a+b+c=\dfrac{1}{2}\\2c=a+b+1\\2a=b+c+2\\2b=a+c-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b+c+1=3c\\a+b+c+2=3a\\a+b+c-3=3b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3c=\dfrac{3}{2}\\3a=\dfrac{5}{2}\\3b=-\dfrac{5}{2}\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}c=\dfrac{1}{2}\\a=\dfrac{5}{6}\\b=-\dfrac{5}{6}\end{matrix}\right.\)
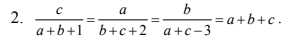 tìm a, b, c
tìm a, b, c