
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nó lừa đấyyyyy :"))
Tài khoản con Mai còn 4 coin thôiiiiiii

Cả đi và về ca nô đi hết số thời gian là:
11h30' - 7h=4h30'=\(\dfrac{9}{2}h\)
Gọi vận tốc của ca nô là: a km/h (a>0)
⇒ vận tốc ca nô khi xuôi dòng là: a+6 (km/h)
vận tốc ca nô khi ngược dòng là: a-6 (km/h) (a>6)
Theo bài ra, ta có pt:
\(\dfrac{36}{a+6}+\dfrac{36}{a-6}=\dfrac{9}{2}\)
\(\dfrac{72a}{a^2-36}=\dfrac{9}{2}\)
\(9a^2-144a-324=0\)
\(\left[\left(3a\right)^2-144a+576\right]=900\)
\(\left(3a-24\right)^2=900\)
\(\Rightarrow\left[{}\begin{matrix}3a-24=30\\3a-24=-30\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=18\left(TM\right)\\a=-2\left(L\right)\end{matrix}\right.\)
Vận tốc của ca nô khi xuôi dòng là: \(18+6=24km\)/h


Ta có A = 4(27 + 297) chia hết cho 4 (1)
Ta lại có A = (29 + 219) - (219 + 229) + ...+ (289 + 299) = (1 + 210) F(x) (F(x) là phần sau không quan trọng lắm nên mình ký hiệu vậy)
Mà 1 + 210 = 1025 chia hết cho 25 (2)
Từ (1) và (2) ta có 29 + 299 chia hết cho 100 (vì 4 và 25 nguyên tố cùng nhau)

bài 2 a, A1 =180-75=105
D= 75 => D1=105
C=60
B=90
b, A1+B1+C1+D1=105+105+60+90=360
C,tổng các góc ngoài của tứ giác bằng 360
bài 3.
a, AB=AD (GT) nên điểm A thuộc dựng trung trực của BD
CB=AD (GT) nên điểm C thuộc đường trung trực của BD
=> AC là đường trung trực của BD
b,
xét tam giác BAC và DAC
BC=CD
AC
AB=AD
=> tam giác BAC=DAC( ccc)
=> B=D ( 2 GÓC TƯƠNG ỨNG )
trong tứ giác ABCD ; A+B+C+D = 360
=> B+D=200
=> B=D=100 độ

6853 + 3153 = ( 685 + 315 ) . ( 8652 + 685 . 315 + 3152 ) = 1 000.
Vì các số hạng trong ngoặc đều chia hết cho 25 nên 8653 + 3153 chia hết cho 25 000.
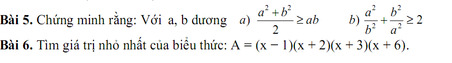


Bài 5:
\(a,\dfrac{a^2+b^2}{2}\ge ab\\ \Leftrightarrow a^2+b^2\ge2ab\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Dấu "=" xảy ra\(\Leftrightarrow a=b\)
\(b,\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}\ge2\\ \Leftrightarrow\dfrac{a^4+b^4}{a^2b^2}\ge2\\ \Leftrightarrow a^4+b^4\ge2a^2b^2\\ \Leftrightarrow a^4-2a^2b^2+b^4\ge0\\ \Leftrightarrow\left(a^2-b^2\right)^2\ge0\)
Dấu "=" xảy ra\(\Leftrightarrow a=b\)
Bài 6:
\(A=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\\ \Rightarrow\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\\ \Rightarrow\left(x^2+5x-6\right)\left(x^2+5x+6\right)\\ \Rightarrow A=\left(x^2+5x\right)^2-36\ge-36\)
Dấu "=" xảy ra \(\Leftrightarrow x^2+5x=0\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(A_{min}=-36\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Bài 5:
a: Ta có: \(\left(a-b\right)^2>=0\)
\(\Leftrightarrow a^2+b^2-2ab>=0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow\dfrac{a^2+b^2}{2}>=ab\)(đpcm)
b: \(\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}\ge2\sqrt{\dfrac{a^2}{b^2}\cdot\dfrac{b^2}{a^2}}=2\)