
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật

\(a^3+3a^2b+3ab^2+b^3-2022=\left(a+b\right)^3-2022=\left(2021-2020\right)^3-2022=1-2022=-2021\)


a) Ta có: \(x^2-3=0\)
nên \(x^2=3\)
hay \(x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
b) Ta có: \(4x^2-9=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
c) Ta có: \(\left(x+2\right)^2-\left(x-2\right)^2=5\)
\(\Leftrightarrow x^2+4x+4-x^2+4x-4=5\)
\(\Leftrightarrow8x=5\)
hay \(x=\dfrac{5}{8}\)
d) Ta có: \(\left(x+2\right)^3-x^3+6x^2=7\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3+6x^2-7=0\)
\(\Leftrightarrow12x^2+12x+1=0\)
\(\Delta=12^2-4\cdot12\cdot1=144-48=96\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-4\sqrt{6}}{24}=\dfrac{-3-\sqrt{6}}{6}\\x_2=\dfrac{-12+4\sqrt{6}}{24}=\dfrac{-3+\sqrt{6}}{6}\end{matrix}\right.\)
e) Ta có: \(\left(x-2\right)^2-\left(x-1\right)\left(x+1\right)=7\)
\(\Leftrightarrow x^2-4x+4-x^2+1=7\)
\(\Leftrightarrow-4x=2\)
hay \(x=-\dfrac{1}{2}\)


a: Ta có: \(2x-3=0\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
b: Ta có: \(\left(2x+7\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=3\end{matrix}\right.\)
c: Ta có: \(2x+7=-3x+32\)
\(\Leftrightarrow5x=25\)
hay x=5
d: Ta có: \(\left(3x-2\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
e: Ta có: \(3x-5=x+7\)
\(\Leftrightarrow2x=12\)
hay x=6
f)ĐK:x≠2,x≠-1
Ta có:\(\dfrac{3}{x-2}=\dfrac{2}{x+1}\)
\(\Rightarrow3\left(x+1\right)=2\left(x-2\right)\)
\(\Leftrightarrow3x+3=2x-4\)
\(\Leftrightarrow x=-7\)

a/ Từ M dựng đường thẳng //BD cắt AC tại E
Xét tg AME có
IA=IM; ID//ME => AD=DE (trong tg đường thẳng đi qua trung điểm 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lại)
Xét tg BCD có
MB=MC; ME//BD => DE=CE (trong tg đường thẳng đi qua trung điểm 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lại)
=> AD=DE=CE Mà AD+DE+CE=AC => AC=3AD
b/ Xét tg AME có IA=IM; AD=DE => ID là đường trung bình của tg AME => \(ID=\frac{ME}{2}\)
Xét tg BCD có MB=MC; DE=CE => ME là đường trung bình của tg BCD => \(ME=\frac{BD}{2}\)
\(\Rightarrow ID=\frac{ME}{2}=\frac{\frac{BD}{2}}{2}=\frac{BD}{4}\)



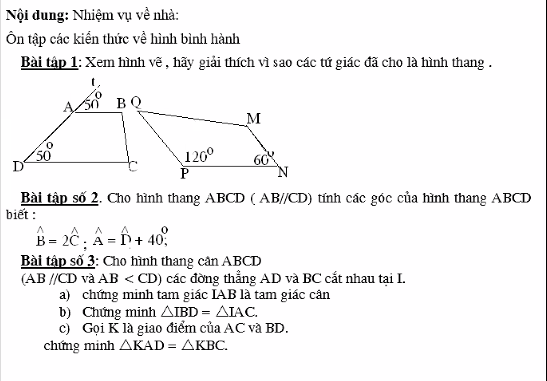
 help mik vs mai phải nộp r;-;
help mik vs mai phải nộp r;-;

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật