Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải:
Giải: Trong không khí vị trí vân sáng bậc 2 là: b 1 = 2 λ D a ; khoảng vân c 1 = λ D a
số vân sáng quan sát được trên màn là:
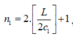
trong đó L là bề rộng trường giao thoa.
Làm thí nghiệm trên trong nước có chiết suất n > 1, với D,a và vị trí của S không đổi thì vị trí vân sáng bậc 2 là:
b
2
=
2
λ
D
n
a
; khoảng vân
c
1
=
λ
D
n
a
; số vân sáng quan sát được trên màn là:
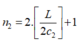
So sánh ta thấy: b1 > b2; c1 >c2; n1 < n2 => chọn B

Chọn đáp án B
Ta có x = x S 4 = 4 λ D a ⇒ λ = a . x 4 D
Trong môi trường chiết suất n = 1,25
⇒ λ ' = λ n ⇒ i ' = i n = λ D a . n ⇒ k = x i ' = 4 λ D a λ D a . n = 4 n = 4.1 , 25 = 5
Vậy tại điểm M vân sáng bậc 4 chuyển thành vân sáng bậc 5

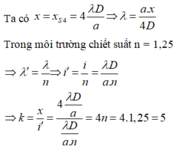
Vậy tại điểm M vân sáng bậc 4 chuyển thành vân sáng bậc 5.
Đáp án C

\(i = \frac{\lambda D}{a}.\)
Thay \(\lambda_{lam}\) bằng \(\lambda_{đỏ}\)
\(\lambda_{đỏ}>\lambda_{lam}\), giữ nguyên D, a => \(i \uparrow\).

Tại vân tối thứ k của 1 bức xạ nào đó có N vân sáng, ta có: \(x=(k+0,5)i=k'.i'\)(*)
Trong môi trường chiết suất n thì bước sóng, khoảng vân giảm đi n lần.
Khi đó, \(i=2i_1;i'=2i_1'\)
Thay vào (*) ta được: \(x=(2k+1)i_1=2k'i_1'\)(**)
Biểu thức (**) đều là điều kiện cho vân sáng.
Như vậy, ta sẽ có (N+1) vân sáng.

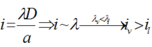
Bề rộng miền giao thoa: \(L=20.i\)
Trong môi trường chiết suất n thì khoảng vân giảm đi n lần, suy ra: \(i'=\dfrac{i}{1,4}\Rightarrow i = 1,4 i'\)
Thế vào trên ta được: \(L=28i'\)
Do vậy, có 28 khoảng vân ứng với 28 vân tối và 29 vân sáng.
Chọn đáp án C
Em cảm ơn ạ ^^