
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
Gọi thời gian hai vòi 1 và 2 chảy một mình đầy bể lần lượt là x,y
Trong 1 giờ, vòi 1 chảy được: 1/x(bể)
Trong 1 giờ, vòi 2 chảy được: 1/y(bể)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\\\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{1}{x}=\dfrac{1}{5}-\dfrac{1}{15}=\dfrac{2}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{15}{2}\\y=15\end{matrix}\right.\)


a: Thay a=-2 vào pt, ta được:
\(-2x^2-2\cdot\left(-2-1\right)x-2+1=0\)
\(\Leftrightarrow-2x^2+6x-1=0\)
\(\Leftrightarrow2x^2-6x+1=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot2\cdot1=36-8=28>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{6-2\sqrt{7}}{2}=3-\sqrt{7}\\x_2=3+\sqrt{7}\end{matrix}\right.\)
b: Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}\left(-2a+2\right)^2-4a\left(a+1\right)>0\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-8a+4-4a^2-4a>0\\a< >0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-12a>-4\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a< >0\\a< \dfrac{1}{3}\end{matrix}\right.\)

\(A=\dfrac{2\sqrt{x}+17}{\sqrt{x+5}}=\dfrac{2\sqrt{x}+10}{\sqrt{x}+5}+\dfrac{7}{\sqrt{x}+5}=2+\dfrac{7}{\sqrt{x}+5}\)
Để \(A\) ∈ \(Z\) thì \(\dfrac{7}{\sqrt{x}+5}\) phải ∈ \(Z\)
=> \(\sqrt{x}+5\) ∈ \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
# Với \(\sqrt{x}+5=-7=>\sqrt{x}=-12\)(Loại)
#Với \(\sqrt{x}+5=-1=>\sqrt{x}=-6\)(Loại)
#Với \(\sqrt{x}+5=1=>\sqrt{x}=-4\left(Loại\right)\)
#Với \(\sqrt{x}+5=7=>\sqrt{x}=2< =>x=4\left(Nhận\right)\)
Vậy \(x=4\) thì \(A\)∈\(Z\)
\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}3\)
\(Ta\) \(Có\) : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}=\sqrt[3]{\dfrac{a^6}{ab.ab\left(a^2-ab+b^2\right)}}=\dfrac{a^2}{\sqrt[3]{ab.ab.\left(a^2-ab+b^2\right)}}\)
\(Áp\) \(dụng\) \(bđt\) \(AM-GM\)
\(\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}\text{≤}\) \(\dfrac{ab+ab+a^2-ab+b^2}{3}\)
\(=>\dfrac{a^2}{\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}}\) \(\text{≥}\) \(\dfrac{3a^2}{a^2+ab+b^2}\) \(Hay\) \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}\text{≥}\dfrac{3a^2}{a^2+ab+b^2}\)
Tương tự ta cũng có :
\(\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\text{≥}\dfrac{3b^2}{b^2+bc+c^2}\)
\(\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+a^2\right)}}\text{≥}\dfrac{3c^2}{a^2+ac+c^2}\)
\(=>\text{}\text{}\)\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\)
Cần c/m \(\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\) ≥ \(1\)
Ta có : \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
\(< =>3a^2\text{≥}a^2+ab+b^2\) \(< =>2a^2-b\left(a+b\right)\text{≥}0\) (1)
Lại có : \(a^2\text{≥}-b\left(a+b\right)\) (2)
Từ (1) và (2) => \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
Tương tự ta cũng có :
\(\dfrac{b^2}{b^2+bc+c^2}\text{≥}\dfrac{1}{3}\)
\(\dfrac{c^2}{a^2+ac+c^2}\text{≥}\dfrac{1}{3}\)
Do đó \(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\text{≥}1\)
Suy ra : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\)
Đẳng thức xảy ra <=> \(a=b=c=1\)

\(\Delta'=16-\left(3m+1\right)\ge0\Rightarrow m\le5\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-8\\x_1x_2=3m+1\end{matrix}\right.\)
Kết hợp điều kiện đề bài ta được: \(\left\{{}\begin{matrix}x_1+x_2=-8\\5x_1-x_2=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-8\\6x_1=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-1\\x_2=-7\end{matrix}\right.\)
Thế vào \(x_1x_2=3m+1\)
\(\Rightarrow\left(-1\right).\left(-7\right)=3m+1\)
\(\Rightarrow m=2\) (thỏa mãn)

15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt

c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)

a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

ĐKXĐ: a khác -1/2 và a>=0 ta có
\(\dfrac{1}{2a-1}.\sqrt{5a^4\left(4a^2-4a+1\right)}=\dfrac{1}{2a-1}.\sqrt{5a^4\left(2a-1\right)^2}=\dfrac{1}{2a-1}\sqrt{5}a^2\left|2a-1\right|\)
TH1 : a>=1/2 :
D=\(\sqrt{5}a^2\)
TH2: a<1/2: D=\(-\sqrt{5}a^2\)
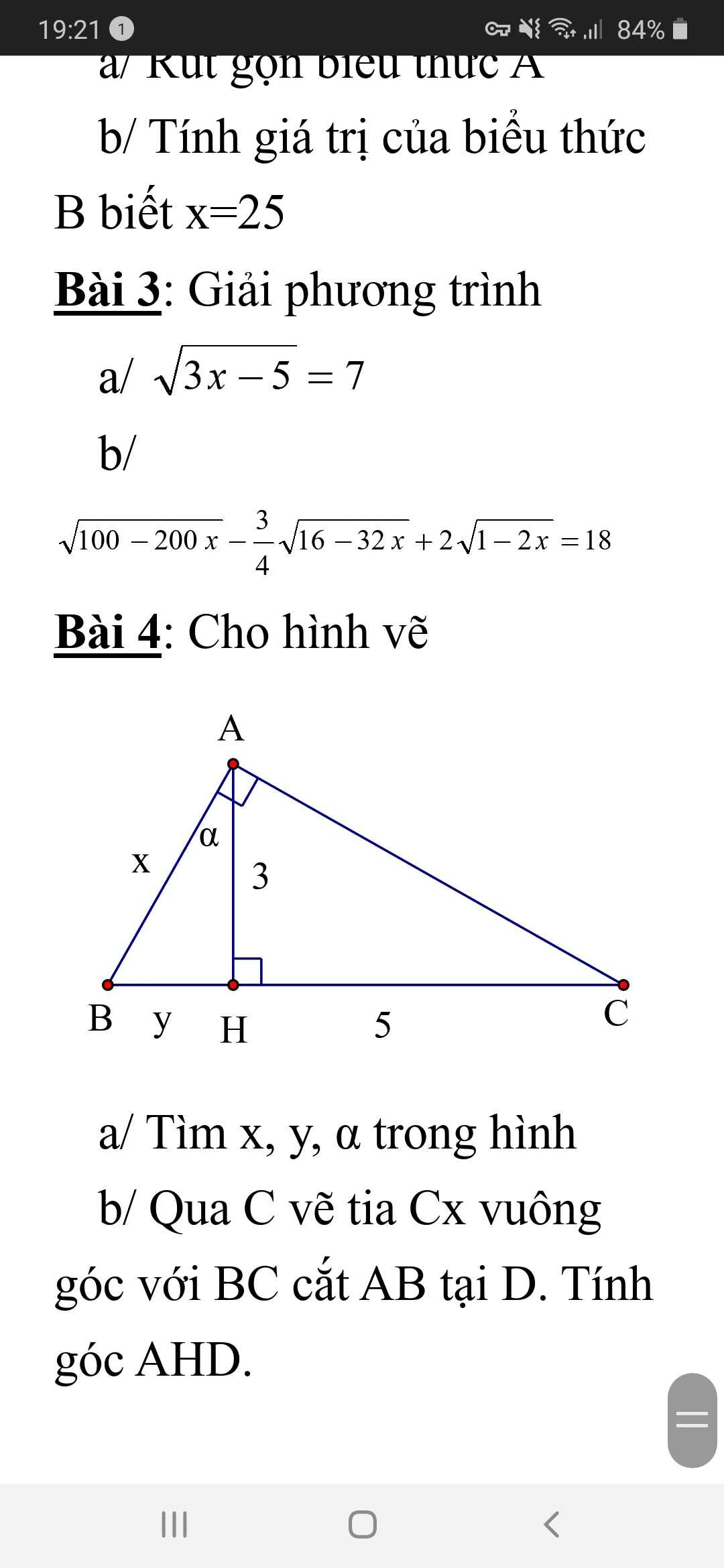





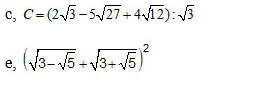
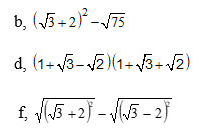 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp

Bài 3:
a: \(\sqrt{3x-5}=7\)
\(\Leftrightarrow3x-5=49\)
\(\Leftrightarrow3x=54\)
hay x=18
Bài 3:
b. \(\sqrt{100-200x}-\dfrac{3}{4}\sqrt{16-32x}+2\sqrt{1-2x}=18\)
<=> \(\sqrt{100\left(1-2x\right)}-\dfrac{3}{4}\sqrt{16\left(1-2x\right)}+2\sqrt{1-2x}=18\)
<=> \(10\sqrt{1-2x}-3\sqrt{1-2x}+2\sqrt{1-2x}=18\)
<=> \(\left(10-3+2\right)\sqrt{1-2x}=18\)
<=> \(11\sqrt{1-2x}=18\)
<=> \(\sqrt{1-2x}=\dfrac{18}{11}\)
<=> 1 - 2x = \(\left(\dfrac{18}{11}\right)^2\)
<=> 1 - 2x = \(\dfrac{324}{121}\)
<=> \(1-\dfrac{324}{121}=2x\)
<=> \(2x=\dfrac{-203}{121}\)
<=> \(x=\dfrac{-203}{242}\)