Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Từ B kẻ BH vuông góc với CD tại H
Dễ thấy tam giác BDC cân tại B vì DH = HC
Mà góc C = 45 độ => Tam giác BDC vuông cân
2/ Dễ dàng chứng minh được ABHD là hình vuông
=> BD là tia phân giác góc D
3/ \(S_{ABCD}=\frac{1}{2}\left(AB+CD\right).AD=\frac{1}{2}\left(2+4\right).2=8\left(cm^2\right)\)

1) do tg ABCD là hình thang cân nên: gocsADC =góc BCD=60
mặt khác AB //CD =>BAD=180-ADB=180-60=120
mà BAD=ABC(vì tg ABCD là hthang cân ) =>ABC=120
2)theo bài ra ta có : AD=AB =>tam giác ADB cân tại A=>ABD =ADB (1)
mặt khác : AB//CD =>ABD=BDC (so le trong) (2)
từ (1) và (2) =>ADB =BDC => BD là tia phân giác của ADC
3) ta có ADB =BDC =ADC/2 =60/2=30 (vì BD là tia phân giác của ADC)
xét tam giác BDC có :BDC + BCD +DBC=180 (ĐL)
mà BDC =30 (cmt) , BCD =60 (câu 1) nên DBC =180-30-60=90 =>tam giác BDC vuông tại B

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

a,kẻ \(AH\bot DC(H\in BC)\)
cm được ABHD là hình chữ nhật suy ra AB=HD=2cm
Mà DH+HC=DC
\(\Rightarrow HC=DC-DH=4-2=2\Rightarrow HC=DH=2cm\)
\(\Rightarrow \Delta DBC\) cân tại B
\(\Rightarrow \angle D_1=\angle C=45^o\Rightarrow \angle DBC=90^o\)
\(\Rightarrow\Delta DBC \) vuông cân tại B
b,Ta có \(\angle D_1+\angle D_2=90^o\Rightarrow \angle D_2=90^o-\angle D_1=90^o-45^o=45^o\)
\(\Rightarrow \angle D_1=\angle D_2 \Rightarrow\) DB là phân giác góc D
c,Ta tính được BH=DH=CH=2cm
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}BH(AB+DC)=\dfrac{1}{2}.2.(2+4)=6cm^2\)
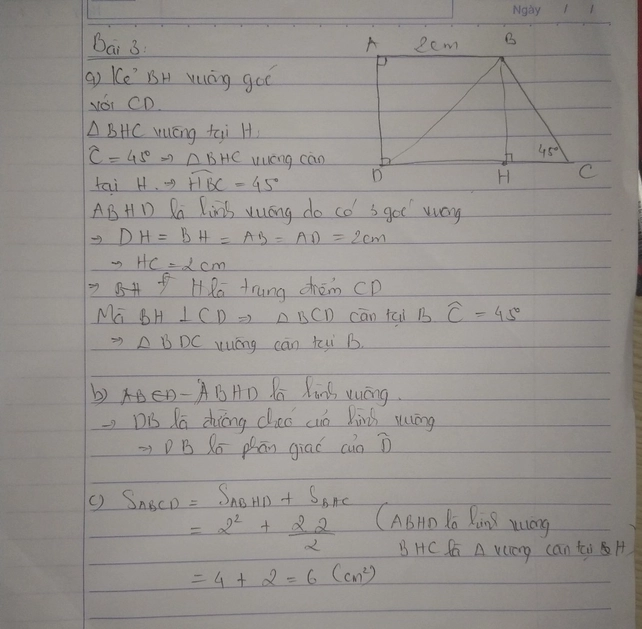
a ) Kẻ BE vuông góc với BD
Xét tứ giác ABED có \(\widehat{DAB}=\widehat{ADE}=\widehat{DEB}=90^o\)
\(\Rightarrow\) ABED là hình vuông
\(\Rightarrow AB=DE\left(1\right)\)
Ta có : CD = DE + EC = 2AB ( 2 )
Từ ( 1 ) và ( 2) \(\Rightarrow DE=EC=AB\)
\(\Rightarrow\) BE là trung tuyến của tam giác BCD
Xét tam giác BCD có BE vừa là đường cao vừa là trung tuyến
\(\Rightarrow\) Tam giác BCD cân tại B
b ) Ta có tứ giác ABED là hình vuông ( chứng minh trên )
\(\Rightarrow\) BD là tia phân giác của \(\widehat{ADE}\) ( tính chất đường chéo của hình vuông )
\(\Rightarrow\) đpcm
Chúc bạn học tốt !!!