K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 3 2022
\(B=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}:\dfrac{3\sqrt{x}-9-2\sqrt{x}+10}{\sqrt{x}-5}\)
\(=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+1}\)
25 tháng 1 2022
Kẻ đường cao AH cho tam giác ABC
sinB = AH/AB => \(\dfrac{\sqrt{3}}{2}=\dfrac{AH}{6}\Rightarrow AH=3\sqrt{3}\)cm
cosB = BH/AB => \(\dfrac{1}{2}=\dfrac{BH}{6}\Rightarrow BH=3cm\)
=> CH = BC - BH = 1 cm
Theo Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=2\sqrt{7}cm\)
-> chọn A
25 tháng 9 2021
1: Xét ΔABC cân tại C có CI là đường trung tuyến ứng với cạnh đáy AB
nên CI là đường cao ứng với cạnh AB
Xét ΔABC cân tại B có BK là đường trung tuyến ứng với cạnh đáy AC
nên BK là đường cao ứng với cạnh AC
2: Xét ΔOBI và ΔOCK có
OB=OC
\(\widehat{IBO}=\widehat{KCO}\left(=60^0\right)\)
IB=KC
Do đó: ΔOBI=ΔOCK
Suy ra: OI=OK
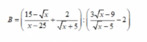
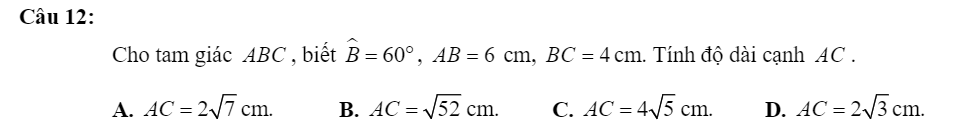
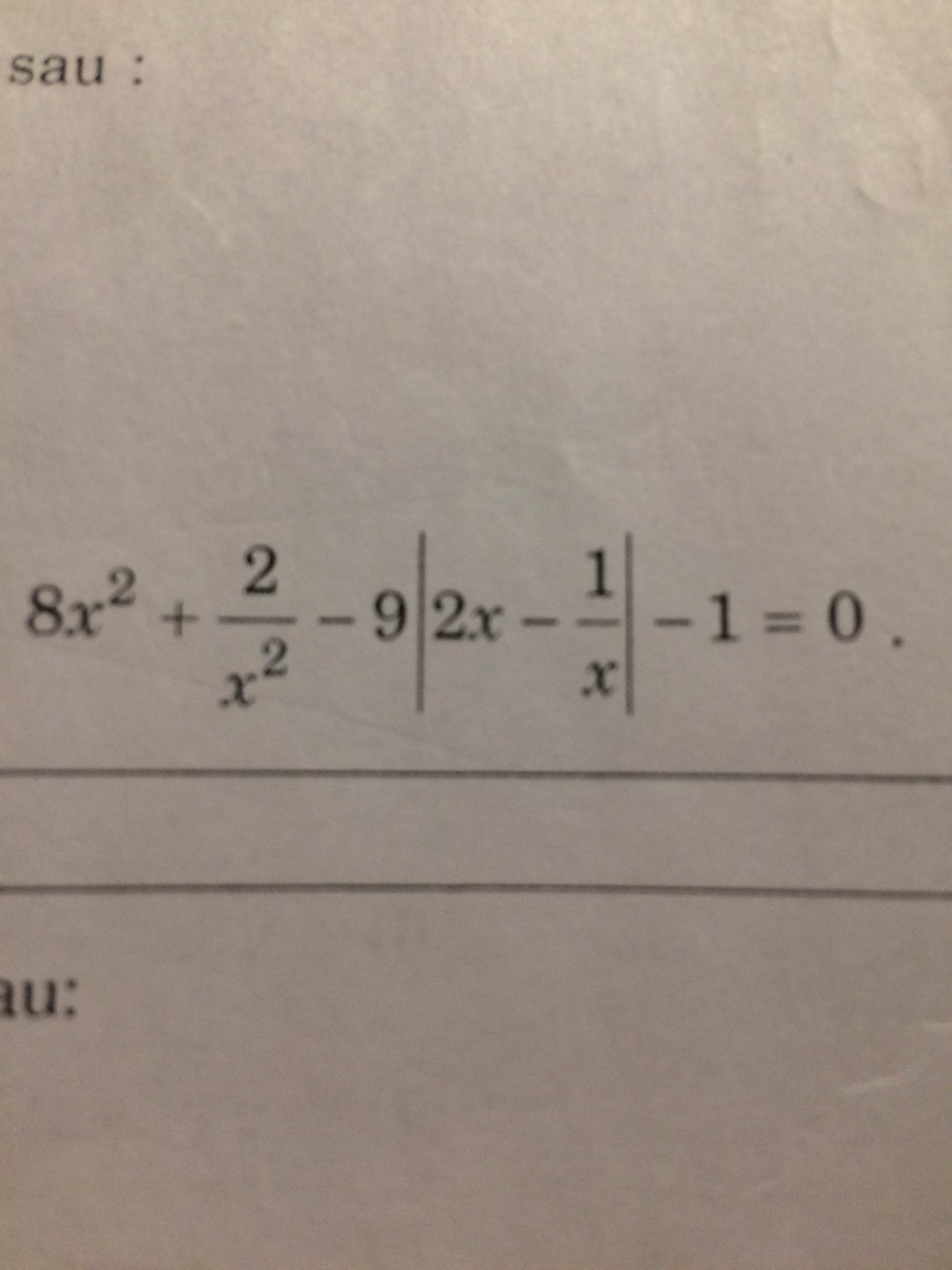
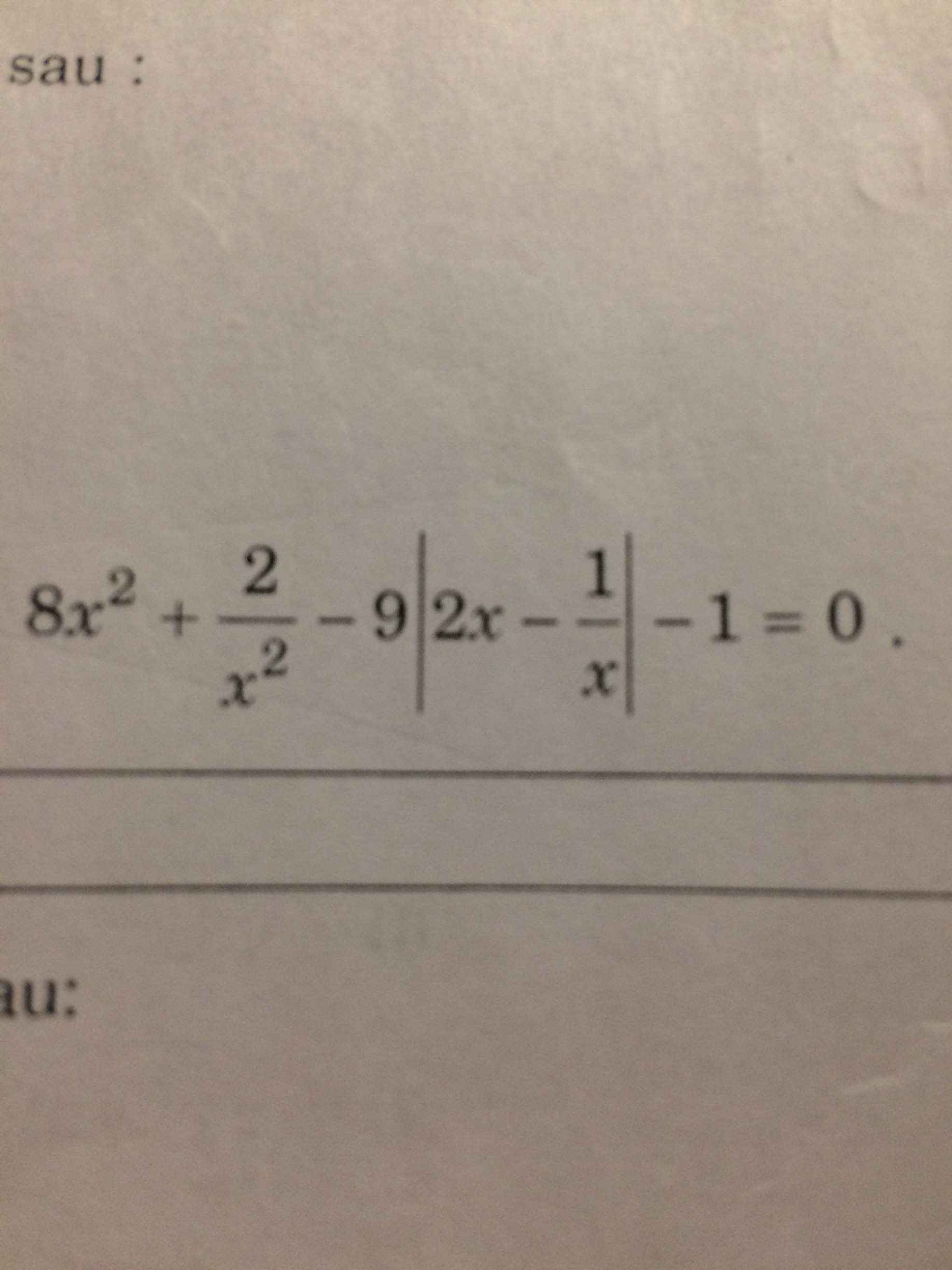
a: \(\Leftrightarrow\sqrt{5-2x}+\dfrac{1}{2}\cdot4\sqrt{5-2x}-5\sqrt{5-2x}=-8\)
\(\Leftrightarrow-2\sqrt{5-2x}=-8\)
=>5-2x=16
=>2x=-11
=>x=-11/2
b: =>x>=0 và 9x^2=10-x
=>x>=0 và 9x^2+x-10=0
=>x=1