
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK:\(x\ge2\)
\(A=x-2\sqrt{x-2}+3=x-2-2\sqrt{x-2}+1+4=\left(\sqrt{x-2}-1\right)^2+4\)Mà ta có \(\left(\sqrt{x-2}-1\right)^2\ge0\)\(\Leftrightarrow\)\(\left(\sqrt{x-2}-1\right)^2+4\ge4\Leftrightarrow A\ge4\)
Dấu bằng xảy ra khi \(\sqrt{x-2}-1=0\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
Vậy GTNN của A là 4
Đây là cách làm của mình thôi, không biết có đúng không.
A = x - 2 \(\sqrt{x}\)- 2+3
= x \(-2\sqrt{x}+1\)
= \((\sqrt{x}-1)^2\)
Mà \((\sqrt{x}-1)^2\ge0\)
=> A \(\ge0\)
Vậy GTNN của A là 0 khi x = 1

a: \(\Leftrightarrow\sqrt{5-2x}+\dfrac{1}{2}\cdot4\sqrt{5-2x}-5\sqrt{5-2x}=-8\)
\(\Leftrightarrow-2\sqrt{5-2x}=-8\)
=>5-2x=16
=>2x=-11
=>x=-11/2
b: =>x>=0 và 9x^2=10-x
=>x>=0 và 9x^2+x-10=0
=>x=1

⇔\(\sqrt{x^2-2x.3+3^2}=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1}\)
⇔\(\sqrt{\left(x-3\right)^2}=\sqrt{\left(\sqrt{3}+1\right)^2}\)
⇔\(\left|x-3\right|=\left|\sqrt{3}+1\right|\)
⇔\(x-3=\sqrt{3}+1\) hoặc \(3-x=\sqrt{3}+1\)
TH1: \(x=\sqrt{3}+4\)
TH2: \(x=2-\sqrt{3}\)
Kiểm tra lại nha ^^

chị khuyên em nên bỏ ý nghĩ đó trong đầu thôi! lo cho xa chứ đừng lo những gì trước mắt ! HẠI THÂN![]()
![]()


Kẻ đường cao AH cho tam giác ABC
sinB = AH/AB => \(\dfrac{\sqrt{3}}{2}=\dfrac{AH}{6}\Rightarrow AH=3\sqrt{3}\)cm
cosB = BH/AB => \(\dfrac{1}{2}=\dfrac{BH}{6}\Rightarrow BH=3cm\)
=> CH = BC - BH = 1 cm
Theo Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=2\sqrt{7}cm\)
-> chọn A


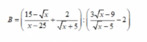


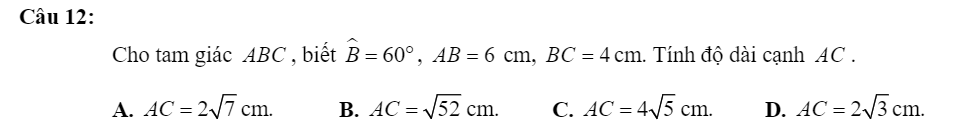
\(B=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}:\dfrac{3\sqrt{x}-9-2\sqrt{x}+10}{\sqrt{x}-5}\)
\(=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+1}\)
nhanh quá