
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c.
ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)
\(1-\dfrac{\sqrt{3}cosx}{sinx}-4cosx=0\)
\(\Rightarrow sinx-\sqrt{3}cosx-4sinx.cosx=0\)
\(\Leftrightarrow sinx-\sqrt{3}cosx=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=sin2x\)
\(\Leftrightarrow sin2x=sin\left(x-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x-\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{4\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{4\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
a.
\(\Leftrightarrow3sin3x-4sin^34x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow sin9x-\sqrt{3}cos9x=2sin2x\)
\(\Leftrightarrow\dfrac{1}{2}sin9x-\dfrac{\sqrt{3}}{2}cos9x=sin2x\)
\(\Leftrightarrow sin\left(9x-\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}9x-\dfrac{\pi}{3}=2x+k2\pi\\9x-\dfrac{\pi}{3}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{21}+\dfrac{k2\pi}{7}\\x=\dfrac{4\pi}{33}+\dfrac{k2\pi}{11}\end{matrix}\right.\)


1.
\(-1\le sin\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=-1\)
\(y_{max}=5\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=1\)
2.
\(-1\le cos2x\le1\Rightarrow\dfrac{5}{2}\le y\le\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi \(cos2x=1\)
\(y_{max}=\dfrac{7}{2}\) khi \(cos2x=-1\)
3.
\(0\le cos^2\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le-1\)
\(y_{min}=-2\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=\pm1\)
\(y_{max}=-1\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=0\)
4.
\(-1\le cos\left(4x^2\right)\le1\Rightarrow-2\le y\le\sqrt{2}-2\)
\(y_{min}=-1\) khi \(cos\left(4x^2\right)=-1\)
\(y_{max}=\sqrt{2}-2\) khi \(cos\left(4x^2\right)=1\)


a.
Kẻ \(AE\perp SD\)
Do \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AE\)
\(\Rightarrow AE\perp\left(SCD\right)\Rightarrow AE=d\left(A;\left(SCD\right)\right)\)
\(AE=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{4a\sqrt[]{5}}{5}\)
\(\left\{{}\begin{matrix}AM\cap\left(SCD\right)=C\\MC=\dfrac{3}{4}AC\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SCD\right)\right)=\dfrac{3}{4}d\left(A;\left(SCD\right)\right)=\dfrac{3a\sqrt{5}}{5}\)
\(\left\{{}\begin{matrix}MN\cap\left(SCD\right)=S\\NS=\dfrac{1}{2}MS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SCD\right)\right)=\dfrac{1}{2}d\left(M;\left(SCD\right)\right)=\dfrac{3a\sqrt{5}}{6}\)
b.
Qua S kẻ tia Sx song song cùng chiều tia DC, trên Sx lấy F sao cho \(SF=DC\)
\(\Rightarrow CDSF\) là hình bình hành \(\Rightarrow CF||SD\Rightarrow\left(SAD\right)||\left(BCF\right)\Rightarrow CD\perp\left(BCF\right)\)
Qua B kẻ \(BG\perp CF\Rightarrow BG\perp\left(SCD\right)\Rightarrow\widehat{BDG}\) là góc giữa BD và (SCD)
SF song song và bằng CD nên SF song song và bằng AB \(\Rightarrow SABF\) là hbh
\(\Rightarrow FB||SA\Rightarrow FB\perp\left(ABCD\right)\) \(\Rightarrow FB\perp BC\)
\(BF=SA=2a\Rightarrow BG=\dfrac{BF.BC}{\sqrt{BF^2+BC^2}}=\dfrac{4a\sqrt{5}}{5}\)
\(BD=\sqrt{AB^2+AD^2}=5a\)
\(\Rightarrow sin\widehat{BDG}=\dfrac{BG}{BD}=\dfrac{4\sqrt{5}}{25}\)
c.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DBA}\) là góc giữa BD và (SAB)
\(tan\widehat{DBA}=\dfrac{AD}{AB}=\dfrac{4}{3}\Rightarrow\widehat{DBA}\)
d.
Từ B kẻ \(BH\perp AC\) (H thuộc AC)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow\widehat{BSH}\) là góc giữa SB và (SAC)
\(BH=\dfrac{AB.BC}{\sqrt{AB^2+BC^2}}=\dfrac{12a}{5}\)
\(\Rightarrow sin\widehat{BSH}=\dfrac{BH}{SB}=\dfrac{12\sqrt{13}}{65}\Rightarrow\widehat{BSH}\)

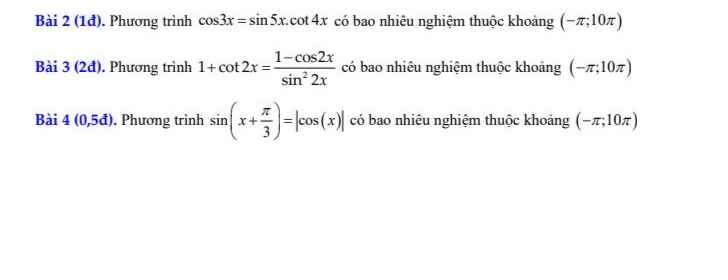


 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ




