Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)


1.
Hàm số xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\cosx-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne k2\pi\end{matrix}\right.\Leftrightarrow x\ne k\pi\)
2.
Hàm số xác định khi:
\(cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
3.
\(cosx+1\ge0\Rightarrow\) Hàm số xác định với mọi x
4.
Hàm số xác định khi:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
5.
Hàm số xác định khi:
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
6.
Hàm số xác định khi:
\(cos3x-cosx\ne0\Leftrightarrow cos3x\ne cosx\Leftrightarrow3x\ne\pm x+k2\pi\Leftrightarrow\left[{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)
\(sin^2x-cos^2x\ne0\Leftrightarrow-cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị

a.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)
b.
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)
\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)

Vận tốc của chất điểm:
\(v\left(t\right)=s'\left(t\right)=3t^2-6t+9=3\left(t-1\right)^2+6\ge6\)
Dấu "=" xảy ra khi \(t-1=0\Rightarrow t=1s\)
Dạ em cảm ơn rất nhiều ạ, nhưng nếu được thầy có thể giải thích giúp em làm sao ra đc :S'(t) ạ ?

Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ


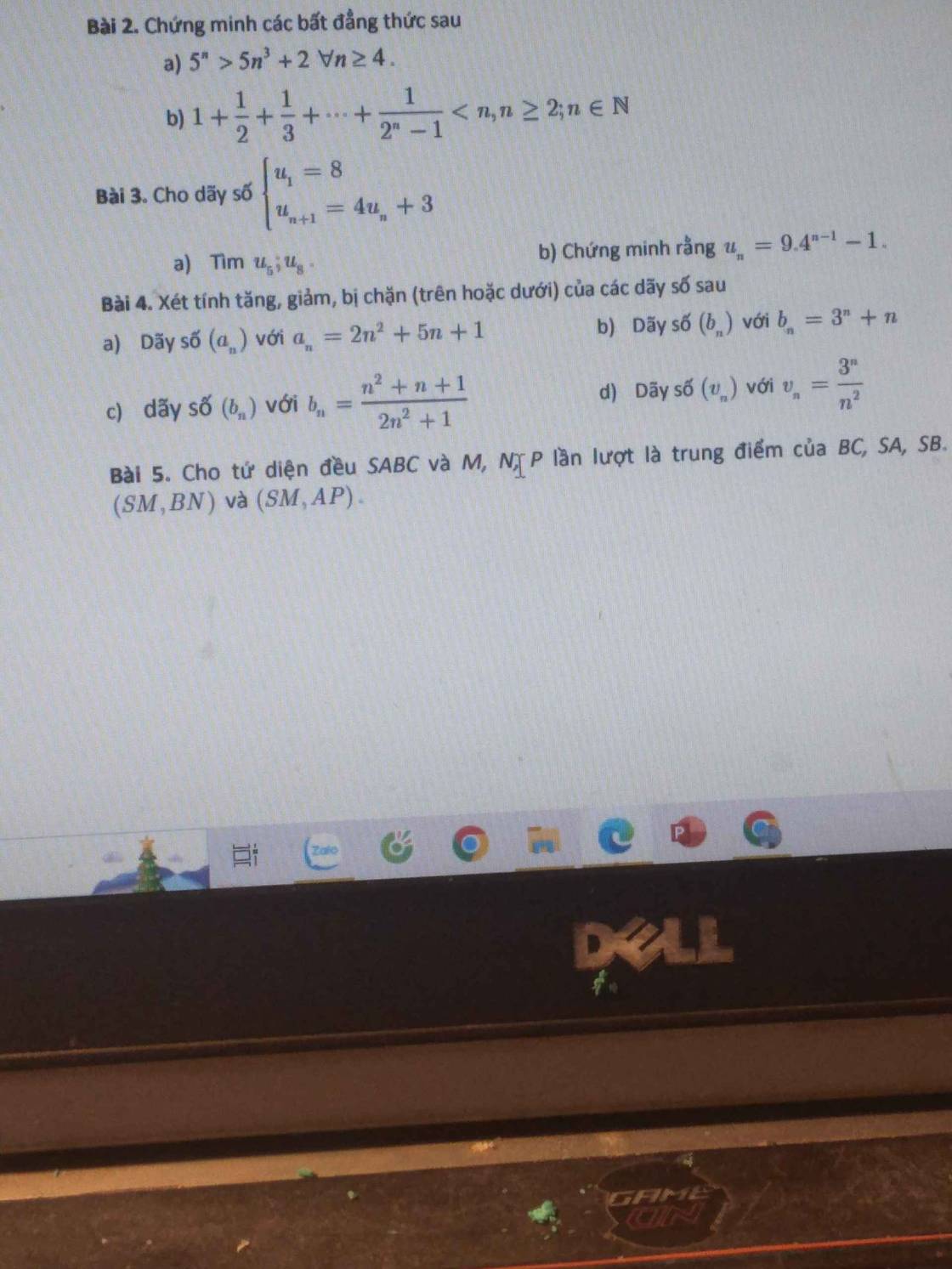 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ