
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{y}}=\dfrac{\sqrt{xy}+y}{y}\)

Bài 2 :
\(\Delta'=m^2-\left(2m-1\right)=\left(m-1\right)^2\ge0\)
Để pt có 2 nghiệm pb
\(m-1\ne0\Leftrightarrow m\ne1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)
Ta có : \(2x_1-3x_2=4\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=2m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=2m-\dfrac{4m-4}{5}=\dfrac{6m+4}{5}\end{matrix}\right.\)
Thay vào (3) ta được \(\left(\dfrac{6m+4}{5}\right)\left(\dfrac{4m+4}{5}\right)=2m-1\)
\(\Rightarrow\left(6m+4\right)\left(4m+4\right)=50m-25\Leftrightarrow24m^2+40m+16=50m-25\)
\(\Leftrightarrow24m^2-10m+41=0\)
\(\Delta'=10-41.24< 0\)Vậy pt vô nghiệm hay ko có gtri m
5.
\(\Delta'=9-\left(2m+1\right)=8-2m>0\Rightarrow m< 4\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2m+1\end{matrix}\right.\)
Kết hợp Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1^2=x_2-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2=6-x_1-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2+x_1-2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=1;x_2=5\\x_1=-2;x_2=8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m+1\Rightarrow\left[{}\begin{matrix}2m+1=5\\2m+1=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{17}{2}\end{matrix}\right.\) (thỏa mãn)



Câu b bạn tự vẽ
Câu c:
PT hoành độ giao điểm: \(-3x+1=\left(1-2m\right)x+m-1\)
Mà 2 đt cắt tại hoành độ 1 nên \(x=1\)
\(\Leftrightarrow-2=1-2m+m-1\Leftrightarrow m=2\)
Câu d:
PT giao Ox,Oy lần lượt tại A,B của (d) là:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{m-1}{2m-1}\Rightarrow A\left(\dfrac{m-1}{2m-1};0\right)\Rightarrow OA=\left|\dfrac{m-1}{2m-1}\right|\\x=0\Rightarrow y=m-1\Rightarrow B\left(0;m-1\right)\Rightarrow OB=\left|m-1\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến (d)
Đặt \(OH^2=t\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{4m^2-4m+2}{\left(m-1\right)^2}\Leftrightarrow t=\dfrac{m^2-2m+1}{4m^2-4m+2}\\ \Leftrightarrow4m^2t-4mt+2t=m^2-2m+1\\ \Leftrightarrow m^2\left(4t-1\right)+2m\left(1-2t\right)+2t-1=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta'=\left(1-2t\right)^2-\left(4t-1\right)\left(2t-1\right)\ge0\\ \Leftrightarrow4t^2-4t+1-8t^2+6t-1\ge0\\ \Leftrightarrow2t-4t^2\ge0\\ \Leftrightarrow2t\left(1-2t\right)\ge0\\ \Leftrightarrow0\le t\le\dfrac{1}{2}\)
\(\Leftrightarrow OH^2\le\dfrac{1}{2}\Leftrightarrow OH\le\dfrac{1}{\sqrt{2}}\)
Dấu \("="\Leftrightarrow\dfrac{m^2-2m+1}{4m^2-4m+2}=\dfrac{1}{2}\Leftrightarrow4m^2-4m+2=2m^2-4m+2\)
\(\Leftrightarrow2m^2=0\Leftrightarrow m=0\)
Vậy m=0 thỏa yêu cầu đề

a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)

a/
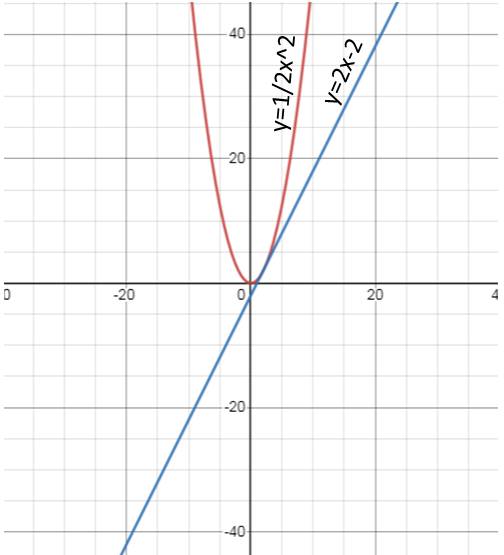
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)

 bài 3 câu c help pls
bài 3 câu c help pls
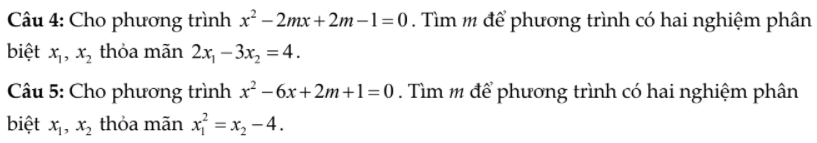


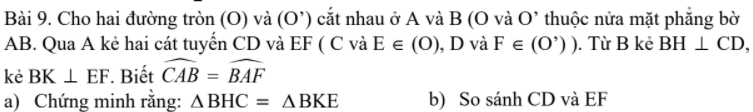


 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
a: Xét tứ giác AICO có
\(\widehat{IAO}+\widehat{ICO}=180^0\)
Do đó: AICO là tứ giác nội tiếp
hay A,I,C,O cùng thuộc 1 đường tròn
b: Xét (O) có
IA là tiếp tuyến có A là tiếp điểm
IC là tiếp tuyến có C là tiếp điểm
Do đó: IA=IC
Xét (O) có
KC là tiếp tuyến có C là tiếp điểm
KB là tiếp tuyến có B là tiếp điểm
Do đó: KC=KB
Ta có: IK=CI+CK
nên IK=IA+BK