
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là câu bđt của chuyên Quảng Nam vừa thi mà:vvv
Ta có: \(xy+yz+zx=xyz\Leftrightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
Đặt \(\left(\frac{1}{x};\frac{1}{y};\frac{1}{z}\right)=\left(a;b;c\right)\left(a,b,c>0\right)\)
Khi đó: \(H=\frac{a}{9b^2+1}+\frac{b}{9c^2+1}+\frac{c}{9a^2+1}\)
\(=\left(a+b+c\right)-\left(\frac{9ab^2}{9b^2+1}+\frac{9bc^2}{9c^2+1}+\frac{9ca^2}{9a^2+1}\right)\)
\(\ge1-\left(\frac{9ab^2}{6b}+\frac{9bc^2}{6c}+\frac{9ca^2}{6a}\right)\)
\(=1-\frac{3}{2}\left(ab+bc+ca\right)\ge1-\frac{3}{2}\cdot\frac{\left(a+b+c\right)^2}{3}=1-\frac{3}{2}\cdot\frac{1}{3}=\frac{1}{2}\)
Dấu "=" xảy ra khi: \(x=y=z=3\)
Vậy Min(H) = 1/2 khi x = y = z = 3

\(\Delta=\left(-2m\right)^2-4\left(2m-10\right)\)
=4m^2-8m+40
=4m^2-8m+4+36=(2m-2)^2+36>0
=>(1) luôn có hai nghiệm phân biệt
x1+x2=2m và 2x1+x2=-4
=>-x1=2m+4 và x1+x2=2m
=>x1=-2m-4 và x2=2m+2m+4=4m+4
x1x2=2m-10
=>(-2m-4)(4m+4)=2m-10
=>-8(m-2)(m+1)=2(m-5)
=>-4(m-2)(m+1)=(m-5)
=>-4(m^2-m-2)=m-5
=>-4m^2+4m+8-m+5=0
=>-4m^2+3m+13=0
=>\(m=\dfrac{3\pm\sqrt{217}}{8}\)

\(\Delta'=m^2-\left(m-1\right)=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy pt luôn có 2 nghiệm pb
Ta có : \(x_1+x_2+2\sqrt{x_1x_2}=4\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow\sqrt{m-1}=2-m\)
đk : m =< 2
TH1 \(m-1=2-m\Leftrightarrow m=\dfrac{3}{2}\)(tm)
TH2 \(m-1=m-2\)( vô lí )
\(\Delta'=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m-1\end{matrix}\right.\)
Để biểu thức \(\sqrt{x_1}+\sqrt{x_2}=2\) xác định \(\Rightarrow x_1;x_2\ge0\Rightarrow\left\{{}\begin{matrix}x_1+x_2\ge0\\x_1x_2\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2m\ge0\\m-1\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
Khi đó:
\(\sqrt{x_1}+\sqrt{x_2}=2\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4\)
\(\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow m+\sqrt{m-1}=2\)
Đặt \(\sqrt{m-1}=t\ge0\Rightarrow m=t^2+1\)
\(\Rightarrow t^2+1+t=2\Rightarrow t^2+t-1=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-1+\sqrt{5}}{2}\\t=\dfrac{-1-\sqrt{5}}{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{m-1}=\dfrac{-1+\sqrt{5}}{2}\Rightarrow m-1=\dfrac{3-\sqrt{5}}{2}\)
\(\Rightarrow m=\dfrac{5-\sqrt{5}}{2}\)

\(\Delta=b^2-4ac=\left(m+1\right)^2+1>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm phân biệt với mọi m
Theo định lí Viet ta có :
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1.x_2=-1\end{matrix}\right.\)
\(2\left|x_1\right|+\left|x_2\right|=3\)
\(\Leftrightarrow\left(2\left|x_1\right|+\left|x_2\right|\right)^2=9\)
\(\Leftrightarrow4x_1^2+x_2^2+4x_1.x_2=9\)

Bài 2 :
\(\Delta'=m^2-\left(2m-1\right)=\left(m-1\right)^2\ge0\)
Để pt có 2 nghiệm pb
\(m-1\ne0\Leftrightarrow m\ne1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)
Ta có : \(2x_1-3x_2=4\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=2m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=2m-\dfrac{4m-4}{5}=\dfrac{6m+4}{5}\end{matrix}\right.\)
Thay vào (3) ta được \(\left(\dfrac{6m+4}{5}\right)\left(\dfrac{4m+4}{5}\right)=2m-1\)
\(\Rightarrow\left(6m+4\right)\left(4m+4\right)=50m-25\Leftrightarrow24m^2+40m+16=50m-25\)
\(\Leftrightarrow24m^2-10m+41=0\)
\(\Delta'=10-41.24< 0\)Vậy pt vô nghiệm hay ko có gtri m
5.
\(\Delta'=9-\left(2m+1\right)=8-2m>0\Rightarrow m< 4\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2m+1\end{matrix}\right.\)
Kết hợp Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1^2=x_2-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2=6-x_1-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2+x_1-2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=1;x_2=5\\x_1=-2;x_2=8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m+1\Rightarrow\left[{}\begin{matrix}2m+1=5\\2m+1=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{17}{2}\end{matrix}\right.\) (thỏa mãn)


\(\Leftrightarrow\left\{{}\begin{matrix}8m+9=41\\m+0=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\m=4\end{matrix}\right.\Leftrightarrow m=4\)

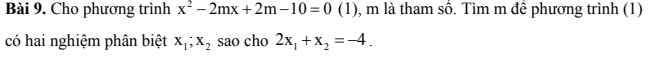
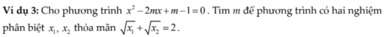
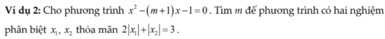
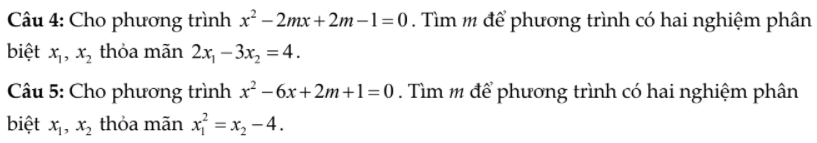

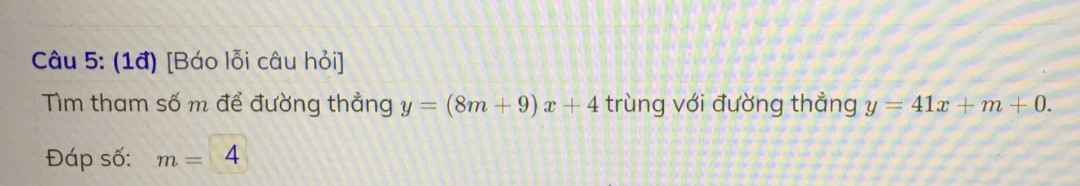
\(\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{y}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{y}}=\dfrac{\sqrt{xy}+y}{y}\)