Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
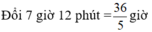
Gọi thời gian người thứ 1 làm một mình xong công việc là x (giờ), (điều kiện x > 0.
Gọi thời gian người thứ 2 làm một mình xong việc là y (giờ), ( điều kiện y > 0).

Vậy thời gian người thứ 1 làm một mình xong công việc là 12 giờ
Thời gian người thứ 2 làm một mình xong công việc là 18 giờ.

Gọi thời gian làm riêng của 2 người làm xong công việc lần lượt a ; b ( a;b > 0 )
1 giờ người thứ nhất làm được 1/a công việc
1 giờ người thứ 2 làm được 1/b công việc
Theo bài ra ta có hệ phương trình \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{6}{x}+\dfrac{3}{y}=\dfrac{2}{3}\end{matrix}\right.\)Đặt 1/x = u ; 1/y = v
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=\dfrac{5}{36}\\6u+3v=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{1}{12}\\v=\dfrac{1}{18}\end{matrix}\right.\)Theo cách đặ x = 12 ; y = 18
Vậy ...

Công suất làm việc mỗi giờ của người thứ nhất, người thứ hai lần lượt là a,b (a,b>0)
Ta lập hpt:
\(\left\{{}\begin{matrix}4a+4b=1\\a+2b=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{6}\\b=\dfrac{1}{12}\end{matrix}\right.\)
Vậy nếu làm một mình người thứ nhất cần 6 giờ để hoàn thành công việc, người thứ hai cần đến 12 giờ để hoàn thành công việc đó.

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{1}{x}=\dfrac{5}{36}-\dfrac{1}{18}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=18\end{matrix}\right.\)

Gọi thời gian người thứ nhất làm riêng xong công việc là x(giờ)
Gọi thời gian người thứ hai làm riêng xong công việc là y(giờ)
Điều kiện: x; y > 0
Trong 1 giờ người thứ nhất làm được 1/x (công việc)
Trong 1 giờ người thứ hai làm được 1/y (công việc)
Vì hai người làm chung trong 15 giờ được 1/6 công việc nên ta có phương trình:
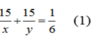
Vì người thứ nhất làm một mình trong 12 giờ và người thứ hai làm một mình trong 20 giờ được 1/5 công việc nên ta có phương trình:
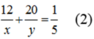
Từ (1) và (2) ta có hệ phương trình:

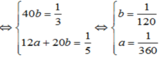
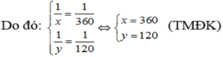
Vậy người thứ nhất làm riêng xong công việc trong 360 giờ; người thứ hai làm riêng xong công việc trong 120 giờ.
Đổi: 7h 12p = \(\frac{36}{5}\)h
Gọi x, y lần lượt là thời gian người thứ nhất; người thứ 2 một mình làm xong công việc ( > 36/5; h )
=> 1 h người thứ nhất làm được: \(\frac{1}{x}\)công việc
1 h người thứ hai làm được \(\frac{1}{y}\)công việc
=> Một h hai người làm được: \(\frac{1}{x}+\frac{1}{y}\) công việc
Theo bài ra 1 h cả hai người làm đươc: 1 : \(\frac{36}{5}\)= \(\frac{5}{36}\)công việc
=> Có phương trình: \(\frac{1}{x}+\frac{1}{y}\)= \(\frac{5}{36}\)(1)
Lại có:
Người thứ nhất làm trong 4h được: \(4.\frac{1}{x}\)công việc
Người thứ 2 làm trong 3 h được: \(3.\frac{1}{y}\)công việc
Thì hai người làm đc 50% công việc
=> \(4.\frac{1}{x}\)+ \(3.\frac{1}{y}\)= \(\frac{1}{2}\)(2)
Từ (1); (2) giải hệ:
\(\hept{\begin{cases}\frac{1}{x}=\frac{1}{12}\\\frac{1}{y}=\frac{1}{18}\end{cases}}\)<=> x = 12; y = 18 ( tm )
Kết luận:...
Đổi 7h 12 phút = 36/5 h
Gọi thời gian người thứ nhất một mình làm xong công việclà x(x>36/5)(h)
thời gian nguời thứ hai một mình làm xong công việc là y (y>36/5)(h)
-Trong 1h
+ Người thứ nhất làm được 1/x (cv)
+ Người thứ hai làm được 1/y (cv )
+ Cả hai người làm được 1: 36/5 = 5/36 (cv)
- Trong 4h, người thứ nhất làm được 4/x (cv)
- Trong 3h, người thứ hai làm được 3/y (cv)
Từ (1) và (2) ta có hệ pt :
Vậy sau 12h người thứ nhất hoàn thành xong công việc
sau 18h người thứ hai hoàn thành xong công việc
\(\text{he pt viet ko }lun\)