
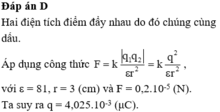
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

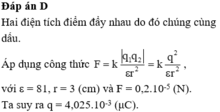

đặc 2 điện tích nói trên là \(q_1\) và \(q_2\) ; theo định luật \(Cu-lông\) ta có :
\(F_1=1,6.10^{-4}=\dfrac{k\left|q_1q_2\right|}{\varepsilon r^2}\) ; \(F_2=2,5.10^{-4}=\dfrac{k\left|q_1q_2\right|}{\varepsilon r_1^2}\)
\(\Rightarrow\dfrac{\dfrac{k\left|q_1q_2\right|}{\varepsilon r^2}}{\dfrac{k\left|q_1q_2\right|}{\varepsilon r_1^2}}=\dfrac{1,6.10^{-4}}{2,5.10^{-4}}\Leftrightarrow\dfrac{r^2}{r_1^2}=\dfrac{16}{25}\Leftrightarrow\dfrac{r}{r_1}=\dfrac{4}{5}\Leftrightarrow r_1=\dfrac{5}{4}r\)
\(\Rightarrow r_1=\dfrac{5}{4}.2=\dfrac{5}{2}=2,5cm\)
vậy để lực tương tác giữa 2 điện tích điểm đó bằng \(F_2=2,5.10^{-4}\) thì khoảng cách giữa chúng là \(2,5cm\)

Chọn: D
Hướng dẫn:
Hai điện tích điểm đẩy nhau do đó chúng cùng dấu.
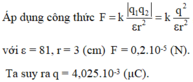

\(\frac{F1}{F2}=\varepsilon\Rightarrow\frac{21}{F2}=2,1\Rightarrow F2=\frac{21}{2,1}=10N\)
Do ban đầu 2 điện tích hút nhau nên lúc sau đổ đầy dầu hỏa vẫn là lực hút chọn A

Lắp công thức vô rồi triển thôi bạn :
a/ Lý luận chút: Giả sử dòng điện dây thứ nhất có hướng từ dưới lên=> vecto cảm ứng từ \(\overrightarrow{B_{1M}}\) có kí hiệu là dấu cộng, tương tự với vecto cảm ứng từ \(\overrightarrow{B_{2M}}\) có kí hiệu là dấu chấm (sử dụng quy tắc bàn tay phải)
Vậy 2 lực tác dụng lên M có hướng ngược chiều nhau
\(B_{1M}=2.10^{-7}.\frac{I_1}{r_1}=2.10^{-7}.\frac{2}{0,05}=8.10^{-6}\left(T\right)\)
\(B_{2M}=2.10^{-7}.\frac{I_2}{r_2}=2.10^{-7}.\frac{4}{0,05}=16.10^{-6}\left(T\right)\)
\(\Rightarrow\sum B=\left|B_{1M}-B_{2M}\right|=\left|8.10^{-6}-16.10^{-6}\right|=8.10^{-6}\left(T\right)\)
b/ N cùng 3 điểm A và B tạo thành 1 tam giác vuông
Lắp công thức vô rồi triển thôi bạn :
a/ Lý luận chút: Giả sử dòng điện dây thứ nhất có hướng từ dưới lên=> vecto cảm ứng từ  có kí hiệu là dấu cộng, tương tự với vecto cảm ứng từ  có kí hiệu là dấu chấm (sử dụng quy tắc bàn tay phải)
Vậy 2 lực tác dụng lên M có hướng ngược chiều nhau
b/ N cùng 3 điểm A và B tạo thành 1 tam giác vuông
Gọi hình nhiếu của N lên dây dẫn 1 là H, lên dây dẫn 2 là K
\(\widehat{NAH}=\widehat{NBA};\sin\widehat{NBA}=\sin\widehat{NAH}=\frac{NA}{AB}=\frac{3}{5}\)
\(\Rightarrow HN=\sin\widehat{NAH}.0,06=\frac{3}{5}.0,06=0,036\left(m\right)\)
\(\sin\widehat{KBN}=\sin\widehat{NAB}=\frac{NB}{AB}=\frac{4}{5}\)
\(\Rightarrow KN=\sin\widehat{KBN}.0,08=\frac{4}{5}.0,08=0,064\left(m\right)\)
\(\Rightarrow B_{1N}=2.10^{-7}.\frac{I_1}{HN}=2.10^{-7}.\frac{2}{0,036}=\frac{1}{90000}\left(T\right)\)
\(\Rightarrow B_{2N}=2.10^{-7}.\frac{I_2}{KN}=2.10^{-7}.\frac{4}{0,064}=\frac{1}{80000}\left(T\right)\)
\(\Rightarrow\sum B=\left|B_{1N}-B_{2N}\right|=\left|\frac{1}{90000}-\frac{1}{80000}\right|=\frac{1}{720000}\left(T\right)\)
c/ \(F_t=2.10^{-7}.\frac{I_1I_2}{r}.l=2.10^{-7}.\frac{2.4}{0,1}.1=16.10^{-6}\left(N\right)\)