Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Theo giả thiết bài toán, ta có:
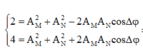
![]()
Áp dụng bất đẳng thức Bunhia cho biểu thức trên
![]()
![]()

Giải thích: Đáp án D
Phương pháp: Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số kết hợp với bất đẳng thức Bu-nhi-a-cốp-xki để đánh giá
Cách giải:
Giả sử phương trình dao động của M và N lần lượt là 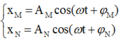
Biên độ dao động tổng hợp của hai dao động trên là: ![]()
Khoảng cách lớn nhất của M và N trên phương Ox là: ![]()
Theo đề bài ta có: 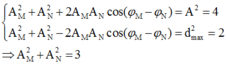
Thấy rằng: 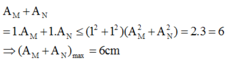

Đáp án C
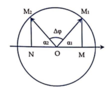 Khoảng cách 2 chất điểm lớn nhất khi M1M2//MN và tứ giác MM1 M2N là hình chữ nhật
Khoảng cách 2 chất điểm lớn nhất khi M1M2//MN và tứ giác MM1 M2N là hình chữ nhật ![]()

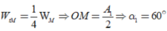
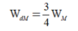
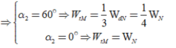


Chọn B.
Khoảng cách giữa M và N là:

Khoảng cách lớn nhất khi MN có phương nằm ngang
⇒ 6 2 + 8 2 = 10 2 ⇒ OM luôn vuông góc với ON. Ở thời điểm mà M có động năng bằng thế năng tại x M = A 2 2
tức OM hợp với Ox góc π / 4 => ON hợp với Ox góc π / 4 hay
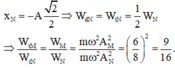

Đáp án C
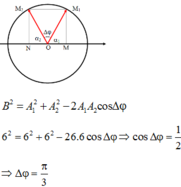
Khoảng cách giữa M và N trong quá trình dao động d = x M − x N = A M 2 + A N 2 − 2 A M A N cos Δ φ cos ω t + ϕ
→ d m a x = A M 2 + A N 2 − 2 A M A N cos Δ φ = 10 cm → Δφ = 0,5π.
Với hai đại lượng vuông pha ta luôn có x M A M 2 + x N A N 2 = 1 , tại E d M = E t M → x M = ± A M 2 x N = ± 3 2 A N → E d M = E t M
Tỉ số động năng của M và N E d M E d N = E M − E t M E N − E t N = A M 2 − 1 2 A M 2 A N 2 − 3 2 A N 2 = A M 2 A N 2 1 − 1 4 1 − 3 4 = 27 16

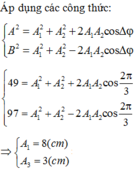

Đáp án D
Theo giả thiết bài toán, ta có:
Áp dụng bất đẳng thức Bunhia cho biểu thức trên