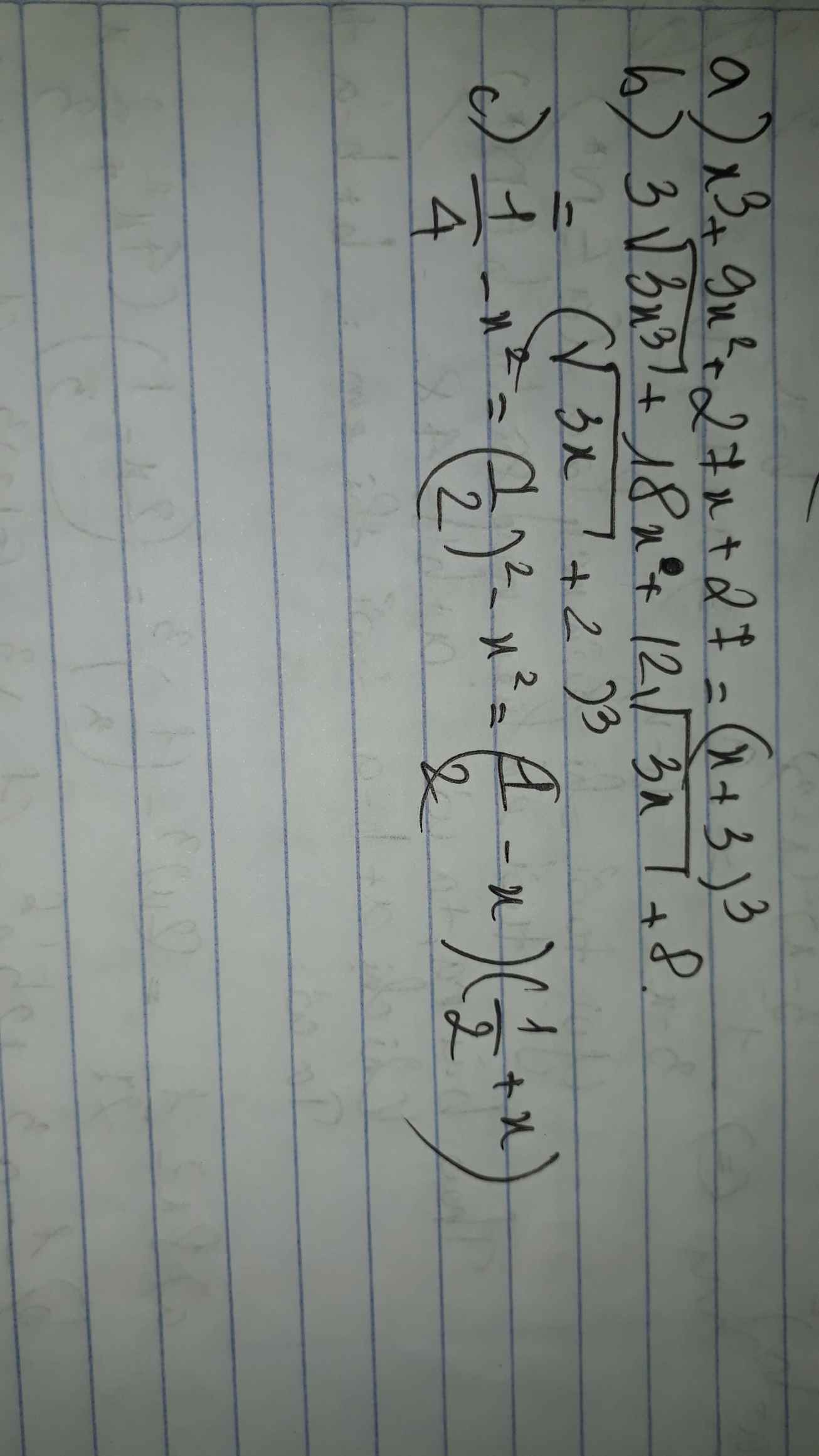NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
3 tháng 5 2017
\(A=\left(\dfrac{6x+4}{3\sqrt{3x^3}-8}-\dfrac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right).\left(\dfrac{1+3\sqrt{3x^3}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
Điều kiện tự làm nha:
Đặt \(\sqrt{3x}=a\) thì ta có:
\(A=\left(\dfrac{2a^2+4}{a^3-8}-\dfrac{a}{a^2+2a+4}\right).\left(\dfrac{1+a^3}{1+a}-a\right)\)
\(=\left(\dfrac{2a^2+4}{\left(a-2\right)\left(a^2+2a+4\right)}-\dfrac{a}{a^2+2a+4}\right).\left(\dfrac{\left(1+a\right)\left(1-a+a^2\right)}{1+a}-a\right)\)
\(=\dfrac{a^2+2a+4}{\left(a-2\right)\left(a^2+2a+4\right)}.\left(1-2a+a^2\right)\)
\(=\dfrac{\left(a-1\right)^2}{a-2}=\dfrac{\left(\sqrt{3x}-1\right)^2}{\sqrt{3x}-2}\)
HP
1
31 tháng 3 2015
xét x=1 không phải là nghiệm của pt
xét x khác 1
\(\left(x-2\right)\left(\sqrt{3x+1}-1\right)=3x\Leftrightarrow\sqrt{3x+1}=\frac{3x}{x-2}+1=\frac{4x-2}{x-2}\)\(;x\ne2\)
\(\Rightarrow3x+1=\frac{16x^2-16x+4}{x^2-4x+4}\Rightarrow\left(3x+1\right)\left(x^2-4x+4\right)=16x^2-16x+4\)
\(\Leftrightarrow3x^3-11x^2+8x+4=16x^2-16x+4\)
\(\Leftrightarrow3x^3-27x^2+24x=0\)
\(\Leftrightarrow x\left(3x^2-27x+24\right)=0\)
\(\Leftrightarrow x.\left(x-8\right)\left(x-1\right)=0\)
- x=0 tmdk
- x=8 tmdf
- x=1 ktmdk
- vậy pt trình có tập nghiệm s={0,8};
MT
0
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
Y
26 tháng 6 2023
\(a,\dfrac{3}{\sqrt{12x-1}}\) xác định \(\Leftrightarrow12x-1>0\Leftrightarrow12x>1\Leftrightarrow x>\dfrac{1}{12}\)
\(b,\sqrt{\left(3x+2\right)\left(x-1\right)}\) xác định \(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}3x+2\ge0\\x-1\ge0\end{matrix}\right.\\\left[{}\begin{matrix}3x+2\le0\\x-1\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\ge-\dfrac{2}{3}\\x\ge1\end{matrix}\right.\\\left[{}\begin{matrix}x\le-\dfrac{2}{3}\\x\le1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{2}{3}\\x\ge1\end{matrix}\right.\)
\(c,\sqrt{3x-2}.\sqrt{x-1}\) xác định \(\Leftrightarrow\left[{}\begin{matrix}3x-2\ge0\\x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{2}{3}\\x\ge1\end{matrix}\right.\) \(\Leftrightarrow x\ge1\)
\(d,\sqrt{\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}}\) xác định \(\Leftrightarrow-x+5>0\Leftrightarrow x< 5\)
