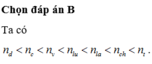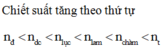Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
Chiết suất của môi trường trong suốt đối với 7 thành phần đơn sắc của ánh sáng: n d o < n c a m < n v a n g < n l u c < n c h a m < n t í m

Ta có công thức:
\(n=a+\dfrac{b}{\lambda^2}\), trong đó a,b là các hằng số phụ thuộc môi trường.
Lập hệ pt \(\Rightarrow\left\{{}\begin{matrix}a=1,484\\b=8,944.10^{-15}\end{matrix}\right.\)
thay số \(\Rightarrow n_{vàng}=a+\dfrac{b}{\left(\lambda_{vàng}\right)^2}=1,484+\dfrac{8,944.10^{-15}}{\left(0,58.10^{-6}\right)^2}=1,51\)

Bề rộng miền giao thoa: \(L=20.i\)
Trong môi trường chiết suất n thì khoảng vân giảm đi n lần, suy ra: \(i'=\dfrac{i}{1,4}\Rightarrow i = 1,4 i'\)
Thế vào trên ta được: \(L=28i'\)
Do vậy, có 28 khoảng vân ứng với 28 vân tối và 29 vân sáng.
Chọn đáp án C

Bước sóng của một ánh sáng đơn sắc trong chân không là \(\lambda\)
Thì bước sóng trong môi trường chiết suất n là \(\lambda_1 = \frac{\lambda}{n}= 600nm.\)
bước sóng trong môi trường chiết suất n' là \(\lambda_2 = \frac{\lambda}{n'}.\)
=> \(\frac{\lambda_2}{\lambda_1}= \frac{n}{n'}=> \lambda_2 =\lambda_1 .\frac{n}{n'} =720nm.\)