K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 2 2022
\(x^2+\sqrt{5}x-10=0\)
\(\Delta=5-4\left(-10\right)=45>0\)
Vậy pt có nghiệm pb
\(x_1=\dfrac{-\sqrt{5}-3\sqrt{5}}{2}=-2\sqrt{5};x_2=\dfrac{-\sqrt{5}+3\sqrt{5}}{2}=\sqrt{5}\)
4 tháng 1 2022
Câu 19:
19.1
Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\widehat{COM}+\widehat{DOM}=\dfrac{1}{2}\cdot180^0=90^0\)
19.2 CM+MD=DC
mà CM=CA
và MD=DB
nên DC=CA+BD
19.3
Xét ΔCOD vuông tại O có OM là đường cao
nên \(OM^2=MC\cdot MD\)
\(\Leftrightarrow R^2=AC\cdot BD\)
Vậy: Tích ACxBD không đổi
TN
Giúp phần a vs ạ tui mất gốc toán
1
14 tháng 3 2022
a)\(\Rightarrow P=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
b) Ta có P=2
\(\dfrac{\Leftrightarrow3\sqrt{x}}{\sqrt{x}+2}=2\Leftrightarrow3\sqrt{x}=2\sqrt{x}+4\)
\(\Leftrightarrow\sqrt{x}=4\Leftrightarrow x=16\left(n\right)\)
Vậy x=16 thì P=2
7 tháng 2 2022
a/ Khi \(m=5\Leftrightarrow\left(d\right):y=6x-5\)
Phương trình hoành độ giao điểm của \(\left(d\right);\left(P\right)\) là :
\(x^2=6x-5\)
\(\Leftrightarrow x^2-6x+5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}M\left(5;25\right)\\N\left(1,1\right)\end{matrix}\right.\) là giao điểm của \(\left(P\right)\) và \(\left(d\right)\) khi \(m=5\)
b/ Phương trình hoành độ giao điểm của \(\left(P\right);\left(d\right)\) là :
\(x^2=\left(m+1\right)x-m\)
\(\Leftrightarrow x^2-\left(m+1\right)+m=0\)
\(\Delta=\left(m+1\right)^2-4m=m^2-2m+1=\left(m+1\right)^2\ge0\)
Để pt có 2 nghiệm pb \(\Leftrightarrow m\ne-1\)
Ta có :
\(y_1-y_2=4\)
\(\Leftrightarrow x_1^2-x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)\left(x_1-x_2\right)=4\)
Theo định lí Viet ta có :
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1.x_2=m\end{matrix}\right.\)
\(\Leftrightarrow x_1-x_2=\dfrac{4}{m+1}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow x_1^2+x_2^2-2x_1.x_2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1.x_2=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(m+1\right)^2-4m=\dfrac{16}{\left(m+1\right)^2}\)
\(\Leftrightarrow\left(m-1\right)^2.\left(m+1\right)^2=16\)
\(\Leftrightarrow\left(m^2-1\right)^2=16\)
\(\Leftrightarrow m^2-1=\pm4\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=3\\m^2=-3\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow m=\pm\sqrt{3}\)
Vậy..
BT
0
RL
1
3 tháng 2 2022
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=3\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=6\\2x-y=3\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(\dfrac{3}{2};0\right)\)
17 tháng 10 2021
a: \(\sqrt{\dfrac{11}{12}}=\dfrac{\sqrt{33}}{6}\)
b: \(\sqrt{\dfrac{\left(\sqrt{3}-\sqrt{2}\right)^2}{5}}=\dfrac{\left(\sqrt{15}-\sqrt{10}\right)}{5}\)
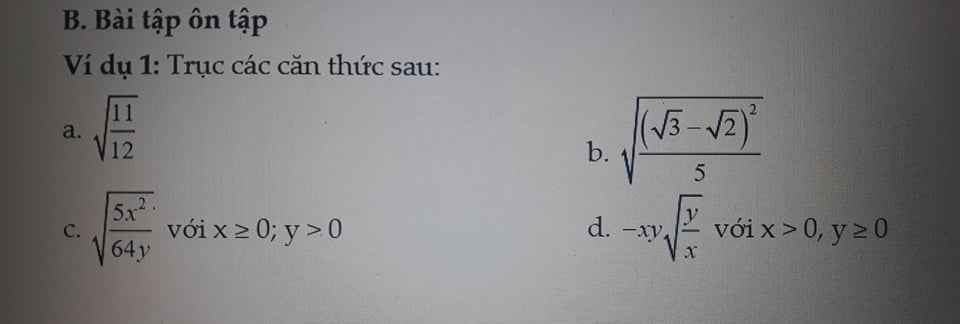
c: \(=\sqrt{5}-\sqrt{3}+\sqrt{5}+\sqrt{3}=2\sqrt{5}\)