
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(m-2\right)x^4-2\left(m+1\right)x^2+2m-1=0\left(1\right)\)
\(m=2\left(ktm\right)\)
\(m\ne2:đặt:x^2=t\ge0\Rightarrow\left(1\right)\Leftrightarrow\left(m-2\right)t^2-2\left(m+1\right)t+2m-1=0\)
\(3nghiem\Leftrightarrow\left\{{}\begin{matrix}2m-1=0\\t1+t2=\dfrac{2m+2}{m-2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m\in\phi\)
\(4nghiem\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\t1+t2>0\Leftrightarrow\\t1.t2>0\end{matrix}\right.\left\{{}\begin{matrix}\left(m+1\right)^2-\left(m-2\right)\left(2m-1\right)>0\\\dfrac{2m+2}{m-2}>0\\\dfrac{2m-1}{m-2}>0\end{matrix}\right.\)
giải hệ bất pt trên=>m
\(c3:b;\left\{{}\begin{matrix}-8\le x\le-2\\m\left(x-3\right)\ge1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le x\le-2\\m\le\dfrac{1}{x-3}\end{matrix}\right.\)
\(có\) \(nghiệm\Leftrightarrow m\le max:\dfrac{1}{x-3}trên\left[-8;-2\right]\)
\(\Leftrightarrow m\le\dfrac{-1}{5}\)



1.
a, \(\left(C\right)x^2+y^2-6x-2y+6=0\)
\(\Leftrightarrow\left(C\right)\left(x-3\right)^2+\left(y-1\right)^2=4\)
\(\Rightarrow\) Tâm \(I=\left(3;1\right)\), bán kính \(R=2\)
b, Tiếp tuyến đi qua A có dạng: \(\left(\Delta\right)ax+by-5a-7b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|3a+b-5a-7b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+3b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow6ab+8b^2=0\)
\(\Leftrightarrow2b\left(3a+4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b=0\\3a+4b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
TH1: \(\Delta_1:x=5\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x=5\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y^2-2y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\Rightarrow\left(5;1\right)\)
TH2: \(\Delta_2:4x-3y+1=0\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}4x-3y+1=0\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{5}\\y=\dfrac{11}{5}\end{matrix}\right.\Rightarrow\left(\dfrac{7}{5};\dfrac{11}{5}\right)\)
Kết luận: Phương trình tiếp tuyến: \(\left\{{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
Tọa độ tiếp điểm: \(\left\{{}\begin{matrix}\left(5;1\right)\\\left(\dfrac{7}{5};\dfrac{11}{5}\right)\end{matrix}\right.\)


Câu 31:
a: vecto ME=vecto MA+vecto AE
=-1/2vecto AB+2/3vecto AC
5 vecto IA+3*vetco IB+4*vecto IC=vecto 0
=>5*vecto IE+5 vecto EA+3 vecto IE+3 vecto EB+4 vecto IE+4 vecto EC=vecto 0
=>12 vecto IE=-5vecto EA-3 vecto EB-4 vecto EC
=>12 vecto IE=10 vecto EC-4 vecto EC-3(vecto EC+vecto CB)
=>12 vecto IE=6 vecto EC-3vecto EC-3 vecto CB
=>12 vecto IE=3 vecto EC-3(vecto CA+vecto AB)
=>12 vecto IE=vecto AC+3 vecto AC-3 vecto AB
=>12 vecto IE=4 vecto AC-3vecto AB
=>vecto IE=-1/4 vecto AB+1/3vecto AC
mà vecto ME=-1/2 vecto AB+2/3vecto AC
nên I là trung điểm của ME
b: vecto AI=vecto AM+vecto MI
=1/2vecto AB+1/2vecto ME
=1/2vecto AB+1/2(-1/2vecto AB+2/3vecto AC)
=1/4vecto AB+1/3vecto AC
vecto AN=vecto AB+vecto BN
=vecto AB+4/7 vecto BC
=vecto AB-4/7vecto AB+4/7vecto AC
=3/7vecto AB+4/7vecto AC
=>A,I,N thẳng hàng

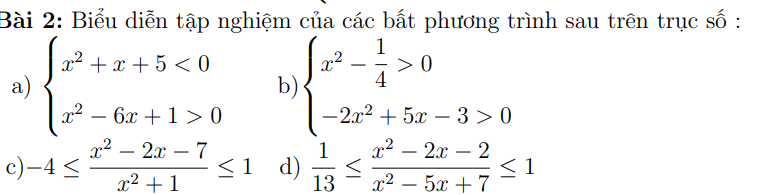
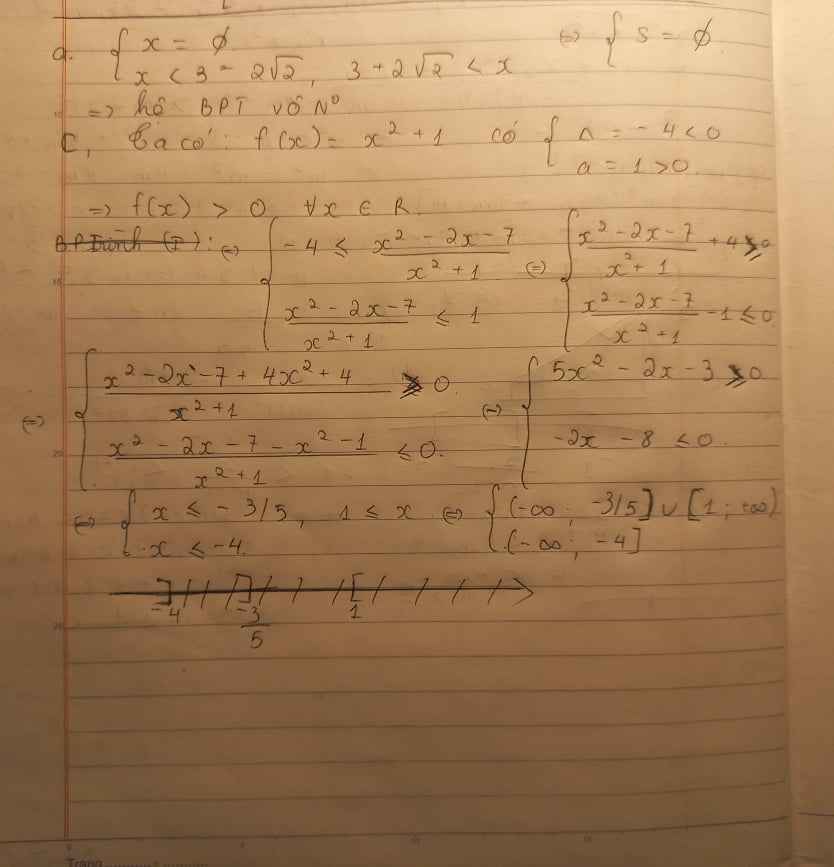

 giúp em câu c và d với ạ 😢
giúp em câu c và d với ạ 😢
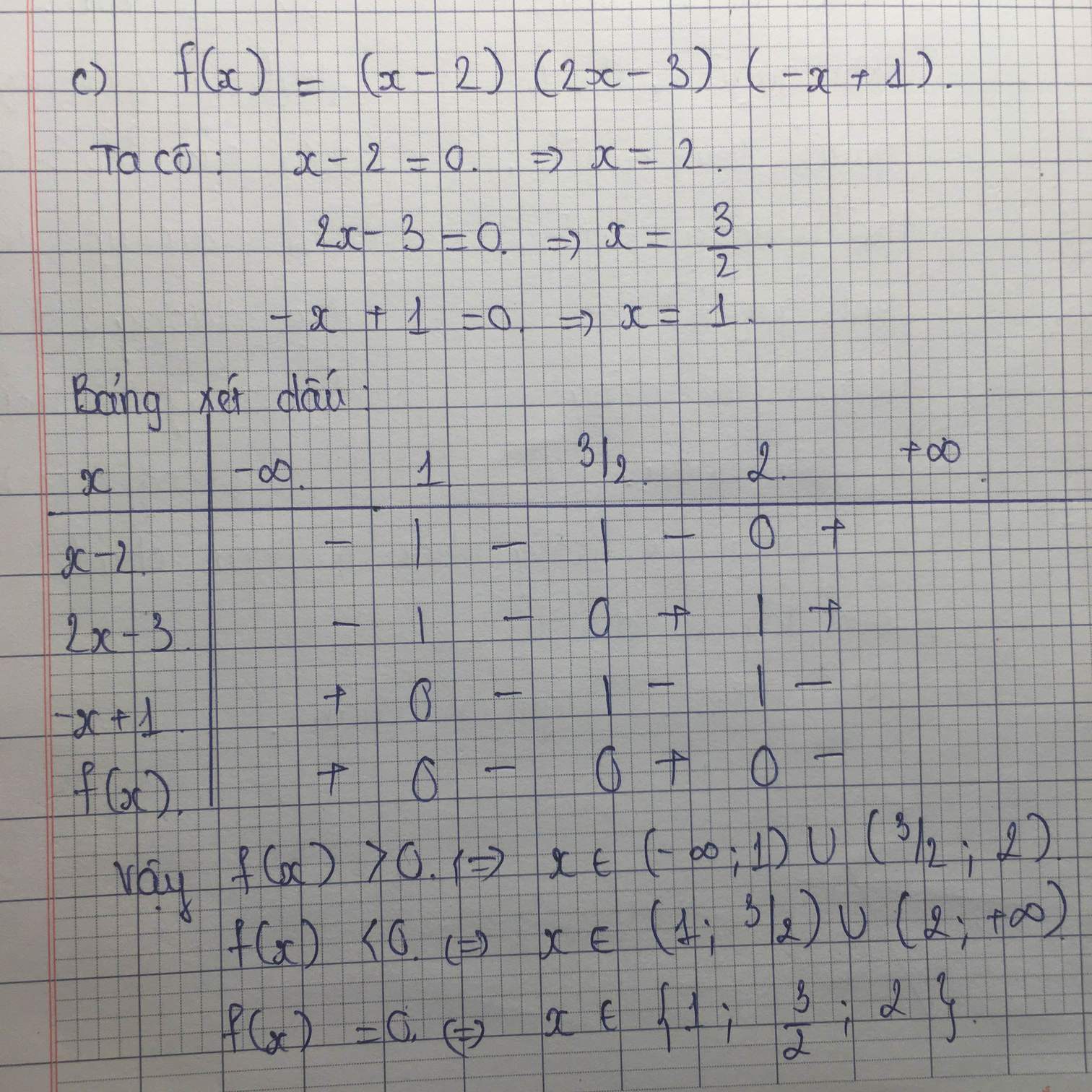


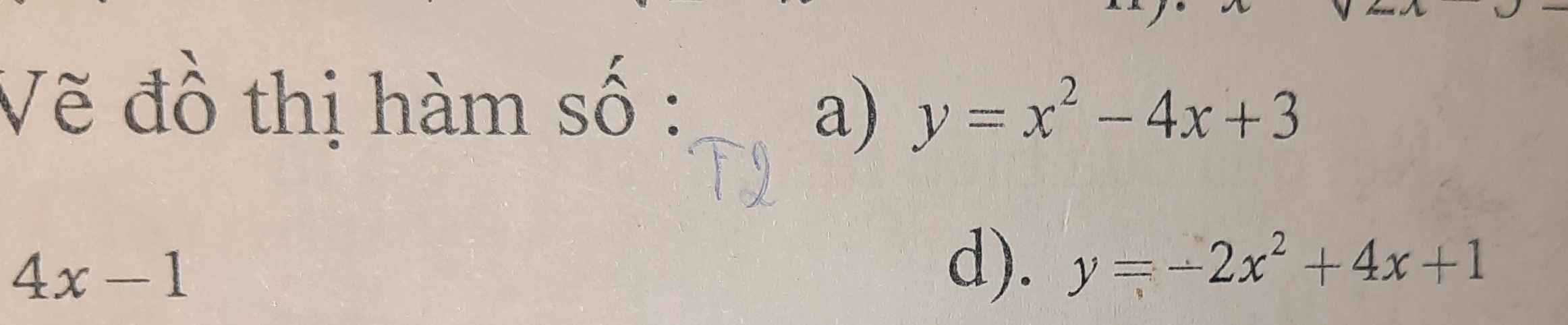



c: \(\Leftrightarrow x^2-5x-x^2-7< =0\)
=>-5x<=7
hay x>=-7/5
d: \(\Leftrightarrow x^2-x-2+3-x^2>=0\)
=>-x+1>=0
=>-x>=-1
hay x<=1