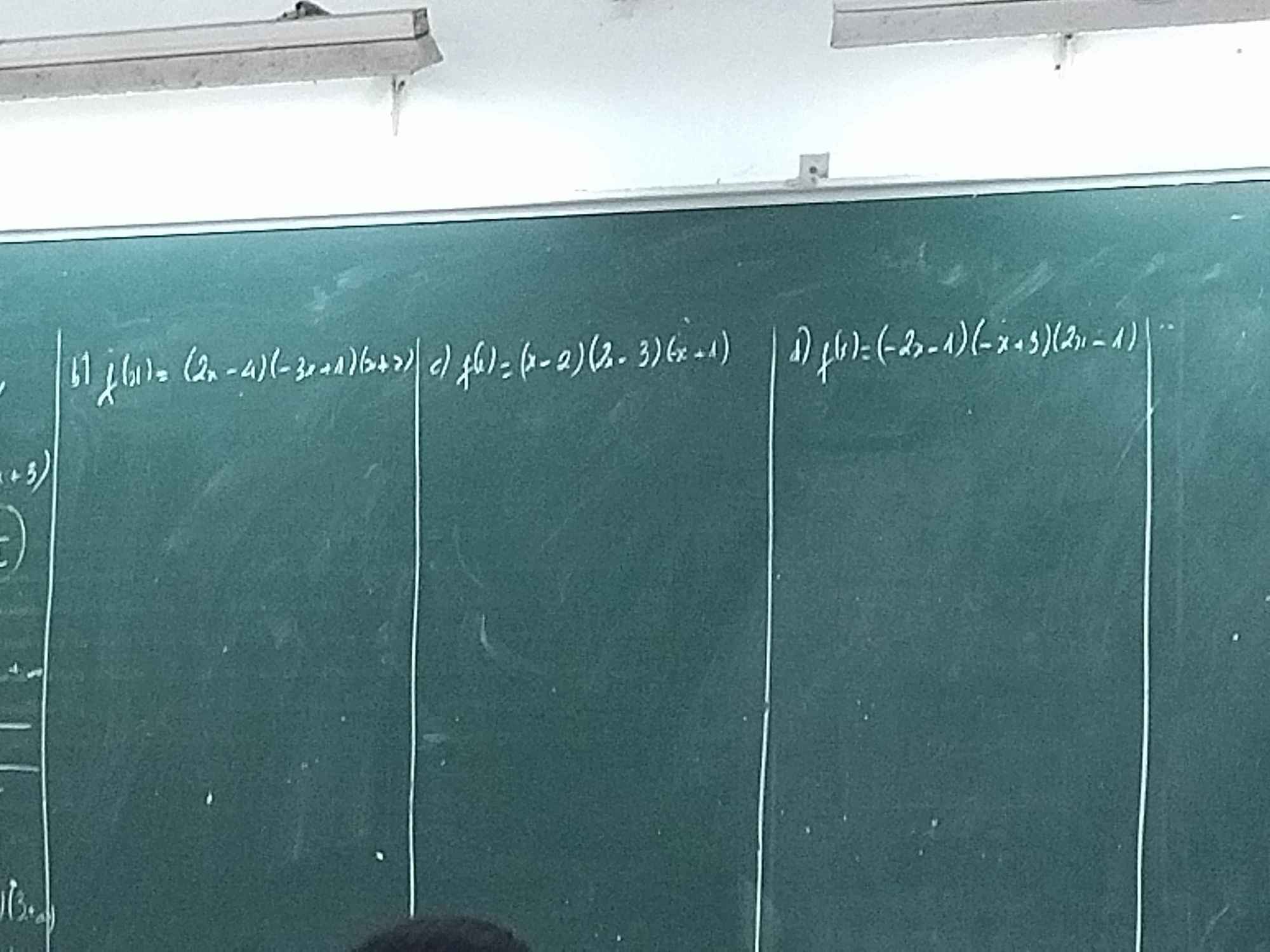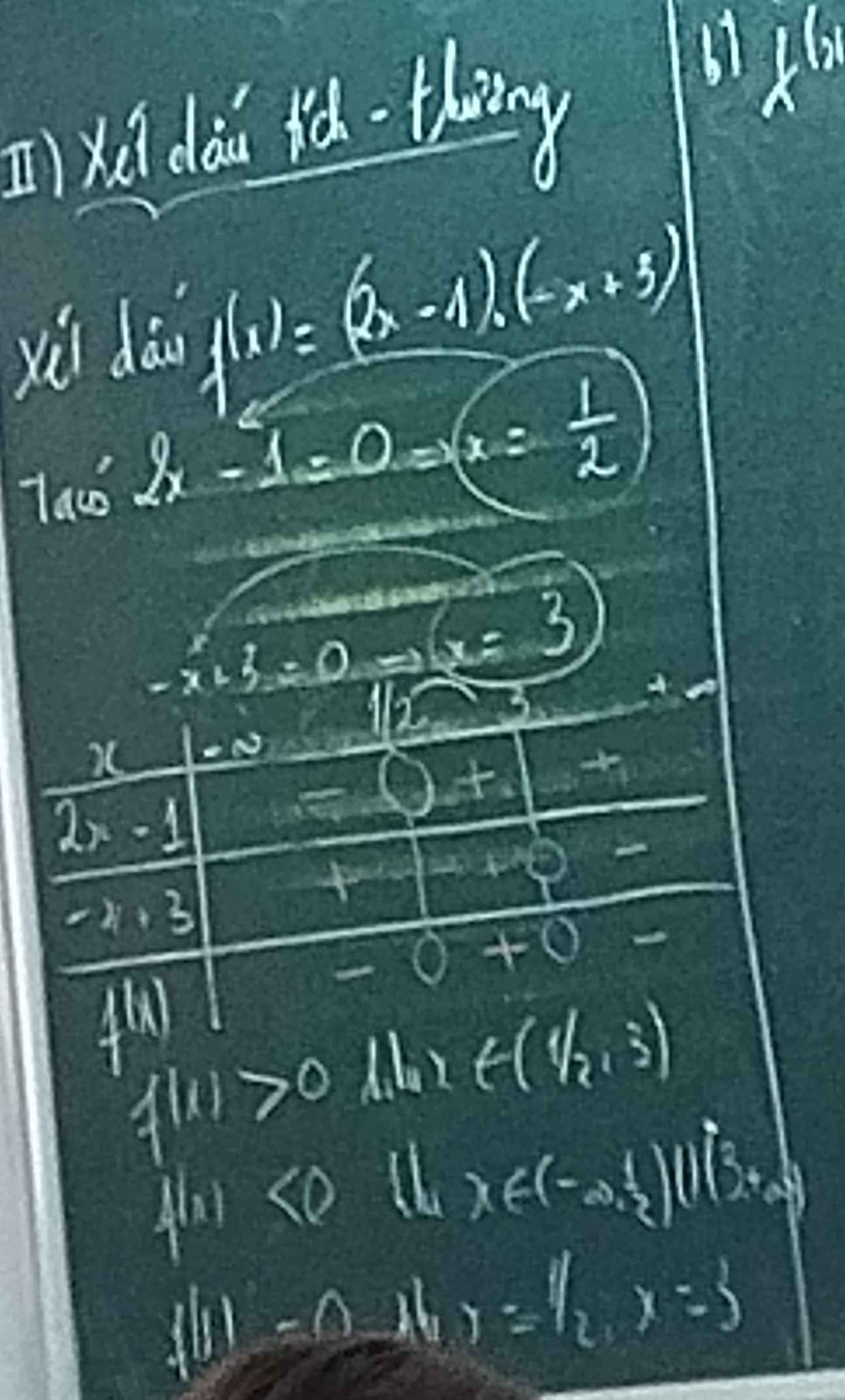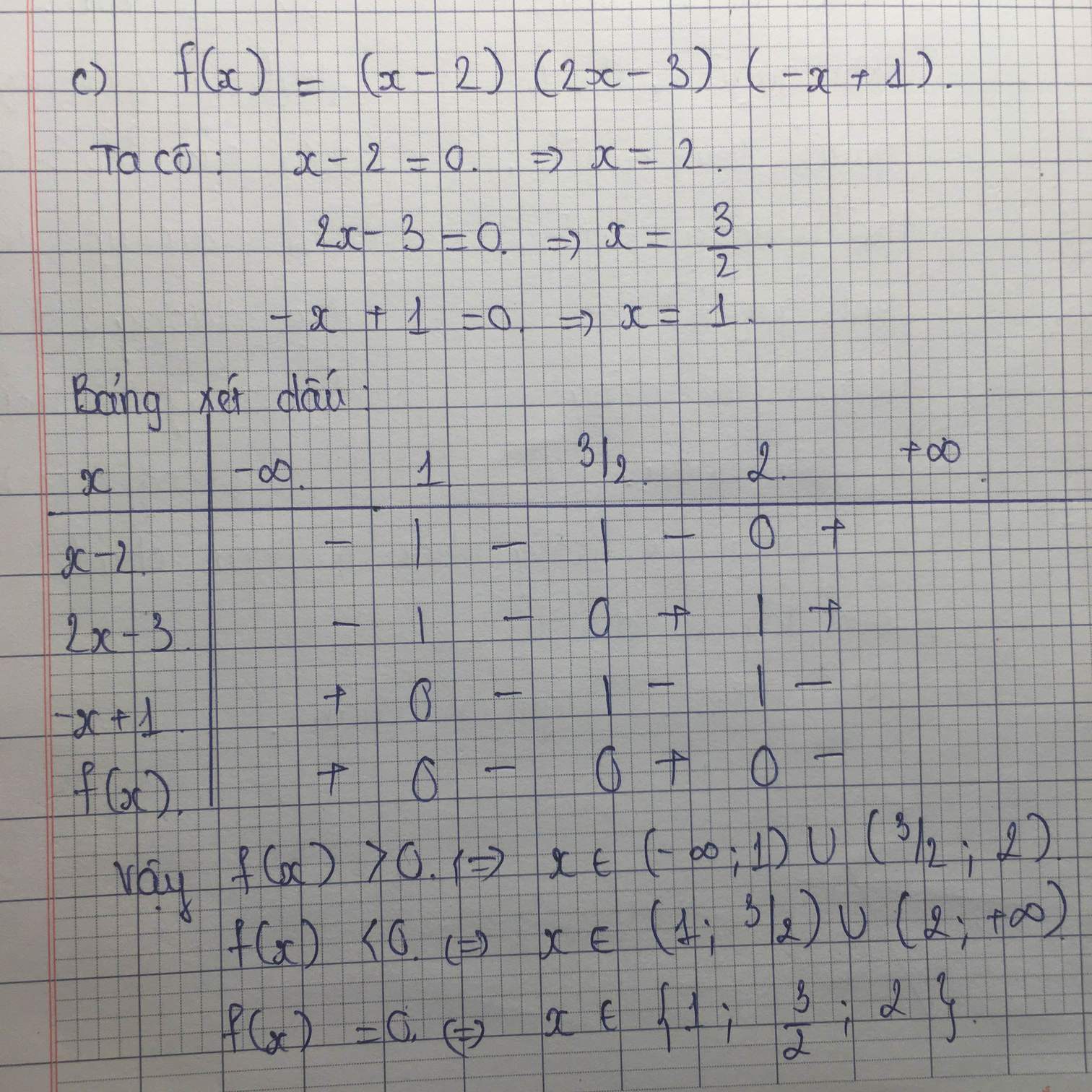giúp em câu c và d với ạ 😢
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BC
0
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 12 2020
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-1\right)\\\overrightarrow{BC}=\left(-3;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{u}=3\overrightarrow{AB}+2\overrightarrow{BC}=\left(-3;5\right)\)
Gọi \(D\left(x;y\right)\Rightarrow\overrightarrow{DC}=\left(1-x;5-y\right)\)
Để ABCD là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x=1\\5-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(0;6\right)\)
22 tháng 11 2021
\(a,\Leftrightarrow\Delta=16+4\left(m+4\right)\left(m-1\right)\ge0\\ \Leftrightarrow4m^2+12m\ge0\\ \Leftrightarrow4m\left(m+3\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-3\end{matrix}\right.\\ b,\Leftrightarrow\Delta=\left(2m+1\right)^2-4\left(m^2+m-6\right)\ge0\\ \Leftrightarrow4m^2+4m+1-4m^2-4m+24\ge0\\ \Leftrightarrow25\ge0\)
Vậy PT luôn có nghiệm với mọi m
\(c,\Leftrightarrow\Delta=\left(m-1\right)^2+40\left(m-1\right)\ge0\\ \Leftrightarrow\left(m-1\right)\left(m+39\right)\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\ge1\\m\le-39\end{matrix}\right.\)
