K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 1 2022
Bài 2:
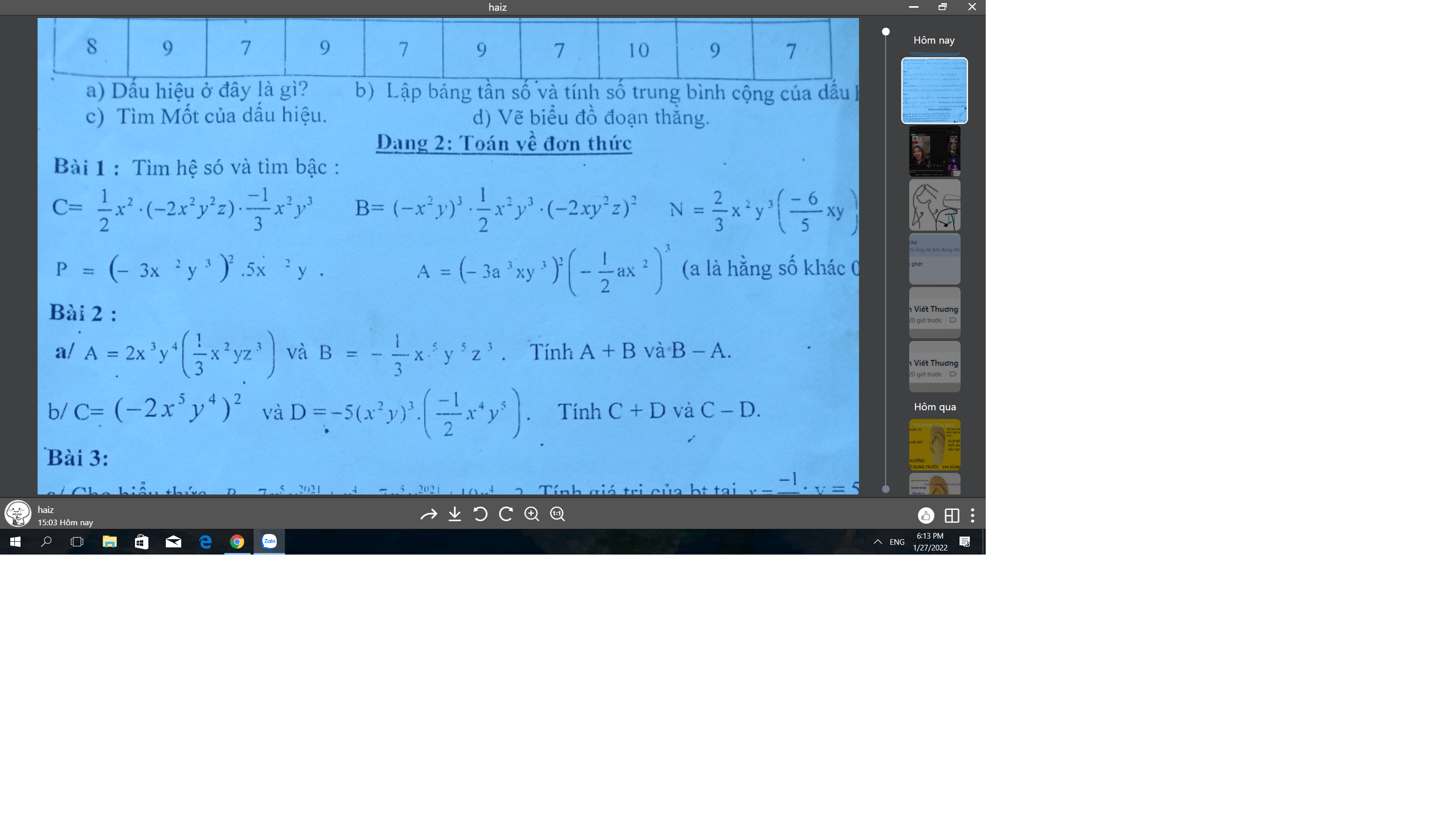
a: \(A+B=\dfrac{2}{3}x^5y^5z^3-\dfrac{1}{3}x^5y^5z^3=\dfrac{1}{3}x^5y^5z^3\)
\(B-A=-\dfrac{1}{3}x^5y^5z^3-\dfrac{2}{3}x^5y^5z^3=-x^5y^5z^3\)
b: \(C+D=4x^{10}y^8+\dfrac{5}{2}x^{10}y^8=\dfrac{13}{2}x^{10}y^8\)
\(C-d=4x^{10}y^8-\dfrac{5}{2}x^{10}y^8=\dfrac{3}{2}x^{10}y^8\)
TM
1
3 tháng 12 2020
Bai lam
\(3^{x+1}=9^x\Leftrightarrow3^{x+1}=3^{2x}\)
\(\Leftrightarrow x-1=2x\Leftrightarrow-x-1=0\Leftrightarrow x=-1\)
22 tháng 1 2022
Bài 2:
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
Suy ra: BD=CD
b: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
hay AD đi qua trung điểm của BC
27 tháng 12 2021
Bài 1:
Gọi số cây 3 lớp 7A,7B,7C lần lượt là \(a,b,c\in \mathbb{N^*},cây\)
Áp dụng tc dtsbn:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{6+4+5}=\dfrac{30}{15}=2\\ \Rightarrow\left\{{}\begin{matrix}a=12\\b=8\\c=10\end{matrix}\right.\)
Vậy ...
Bài 3:
\(a+b\ne-c\Rightarrow a+b+c\ne0\\ \Rightarrow\dfrac{a+b-c}{c}=\dfrac{b+c-a}{a}=\dfrac{c+a-b}{b}=\dfrac{a+b+c}{a+b+c}=1\\ \Rightarrow\left\{{}\begin{matrix}a+b-c=c\\b+c-a=a\\c+a-b=b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b=2c\\b+c=2a\\c+a=2b\end{matrix}\right.\\ \Rightarrow P=\dfrac{a+b}{a}\cdot\dfrac{a+c}{c}\cdot\dfrac{b+c}{b}=\dfrac{2a\cdot2b\cdot2c}{abc}=8\)
NH
29 tháng 3 2020
Bài 3: Bảng giá trị:
| x | -9,5 -6,5 -2,5 |
| x + 2,5 | - | - | - 0 + |
| x + 6,5 | - | - 0 + | + |
| x + 9,5 | - 0 + | + | + |
+) Với x < -9,5
Ta có: -x - 2,5 + (-x) - 6,5 + (-x) - 9,5 = 7
=> -3x - 18,5 = 7
=> -3x = 25,5
=> x = -8,5 (ko thỏa mãn)
+) Với -9,5 ≤ x < -6,5
Ta có: -x - 2,5 + (-x) - 6,5 + x + 9,5 = 7
=> -x + 0,5 = 7
=> -x = 6,5
=> x = -6,5 (ko thỏa mãn)
+) Với -6,5 ≤ x < -2,5
Ta có: -x - 2,5 + x + 6,5 + x + 9,5 = 7
=> x + 13,5 = 7
=> x = -6,5 (thỏa mãn)
+) Với -2,5 ≤ x
Ta có: x + 2,5 + x + 6,5 + x + 9,5 = 7
=> 3x + 18,5 = 7
=> 3x = -11,5
=> x = -23/6 = -3,8(3) (không thỏa mãn)
Vậy x = -6,5
Bài 4: Vì \(\left|x+1\right|\ge0\)\(\forall x\inℝ\); \(\left|x+2\right|\ge0\)\(\forall x\inℝ\) ; ..... ; \(\left|x+100\right|\ge0\)\(\forall x\inℝ\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|+....+\left|x+100\right|\ge0\) \(\forall x\inℝ\) (1)
\(\Rightarrow605x\ge0\)
\(\Rightarrow x\ge0\)\(\Rightarrow\hept{\begin{cases}x+1>0\Rightarrow\left|x+1\right|=x+1\\....\\x+100>0\Rightarrow\left|x+100\right|=x+100\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|+....+\left|x+100\right|=605x\)
\(\Rightarrow x+1+x+2+...+x+100=605x\)
\(\Rightarrow\left(x+x+...+x\right)+\left(1+2+...+100\right)=605x\)
\(\Rightarrow100x+\frac{\left(1+100\right).\left[\left(100-1\right)\div1+1\right]}{2}=605x\)
\(\Rightarrow5050=605x-100x\)
\(\Rightarrow505x=5050\)
\(\Rightarrow x=10\)
