
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)

Đặt \(\frac{3m^2-2m+1}{\left(m+1\right)^2}=a\)\(\Leftrightarrow3m^2-2m-1=a\left(m+1\right)^2=am^2+2am+a\)
\(\Leftrightarrow3m^2-am^2-2m-2am+1-a=0\)
\(\Leftrightarrow\left(3-a\right)m^2-\left(2+2a\right)m+1-a=0\)
\(\Delta=\left(2+2a\right)^2-4\left(1-a\right)\left(3-a\right)=24a-8\)
Để pt có nghiệm:\(24a-8\ge0\Leftrightarrow a\ge\frac{1}{3}\)
Vậy bt ban đầu đạt GTNN là 1/3 khi m=1/2



\(=\sqrt{3\left(x^2-2x+1\right)+25}\supseteq\sqrt{3\left(x+1\right)^2+25}\supseteq5\)
min=5 <=>x=-1
\(\text{Đặt }A=\sqrt{3x^2-6x+28}=\sqrt{3x^2-6x+3+25}\)
\(=\sqrt{3.\left(x^2-2x+1\right)+25}=\sqrt{3.\left(x-1\right)^2+25}\)
\(\Rightarrow A^2=3.\left(x-1\right)^2+25\ge25\Rightarrow A\ge\sqrt{25}=5\)
Dấu "=" xảy ra khi : x=1
Vậy GTNN của A là 5 tại x=1

a) Ta có: \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Thay \(x=4+2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}=\dfrac{2\sqrt{3}+3}{3}\)
c) Để Q=3 thì \(\sqrt{x}+1=3\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\sqrt{x}=-3-1\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
d) Để \(Q>\dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ, ta được: x>1
e) Để Q nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)

\(21,B\\ 22,B\\ 23,C\\ 24,A\\ 25,B\\ 16,C\\ 17,C\\ 18,D\\ 19,B\\ 20,A\)
Hóa bạn qua bên box Hóa đăng nhé

a) \(A=\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}}\Rightarrow A^2=12-3\sqrt{7}+12+3\sqrt{7}-2\sqrt{\left(12-3\sqrt{7}\right)\left(12+3\sqrt{7}\right)}\Rightarrow A^2=24-2\sqrt{144-63}\Rightarrow A^2=24-18\Rightarrow A^2=6\Rightarrow A=\pm\sqrt{6}\)Ta có \(12-3\sqrt{7}< 12+3\sqrt{7}\Rightarrow\sqrt{12-3\sqrt{7}}< \sqrt{12+3\sqrt{7}}\Rightarrow\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}}< 0\Rightarrow A< 0\)Vậy A=-6
b) \(B=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\Rightarrow B^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\Rightarrow B^2=8+2\sqrt{16-10-2\sqrt{5}}\Rightarrow B^2=8+2\sqrt{5-2\sqrt{5}+1}\Rightarrow B^2=8+2\sqrt{\left(\sqrt{5}-1\right)^2}\Rightarrow B^2=8+2\sqrt{5}-2\Rightarrow B=\pm\sqrt{5+2\sqrt{5}+1}\Rightarrow B=\pm\left(\sqrt{5}+1\right)\)Ta có B>0⇒B=\(\sqrt{5}+1\)
c) \(C=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\Rightarrow C^2=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\Rightarrow C^2=6+2\sqrt{9-5}\Rightarrow C^2=6+4=10\Rightarrow C=\pm\sqrt{10}\)Ta có C>0⇒C=\(\sqrt{10}\)

4.
a, \(A=\sqrt[3]{15\sqrt{3}+26}=\sqrt[3]{\left(\sqrt{3}+2\right)^3}=\sqrt{3}+2\)
b, \(B=\sqrt[3]{5+2\sqrt{13}}+\sqrt[3]{5-2\sqrt{13}}\)
\(\Rightarrow2B=\sqrt[3]{40+16\sqrt{13}}+\sqrt[3]{40-16\sqrt{13}}\)
\(=\sqrt[3]{\left(\sqrt{13}+1\right)^3}+\sqrt[3]{\left(\sqrt{13}-1\right)^3}\)
\(=\sqrt{13}+1+\sqrt{13}-1=2\sqrt{13}\)
\(\Rightarrow B=\sqrt{13}\)
c, \(C=\sqrt[3]{182-\sqrt{33125}}+\sqrt[3]{182+\sqrt{33125}}\)
\(\Rightarrow C^3=364+3\sqrt[3]{182-\sqrt{33125}}.\sqrt[3]{182+\sqrt{33125}}\left(\sqrt[3]{182-\sqrt{33125}}+\sqrt[3]{182+\sqrt{33125}}\right)\)
\(=364-3C\)
\(\Rightarrow C^3+3C-364=0\)
\(\Leftrightarrow C=7\)

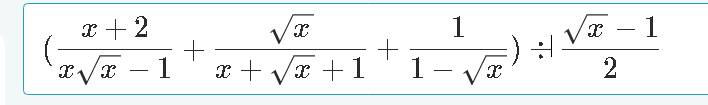 giúp mjk vs mjk đg cần gấp ạ
giúp mjk vs mjk đg cần gấp ạ 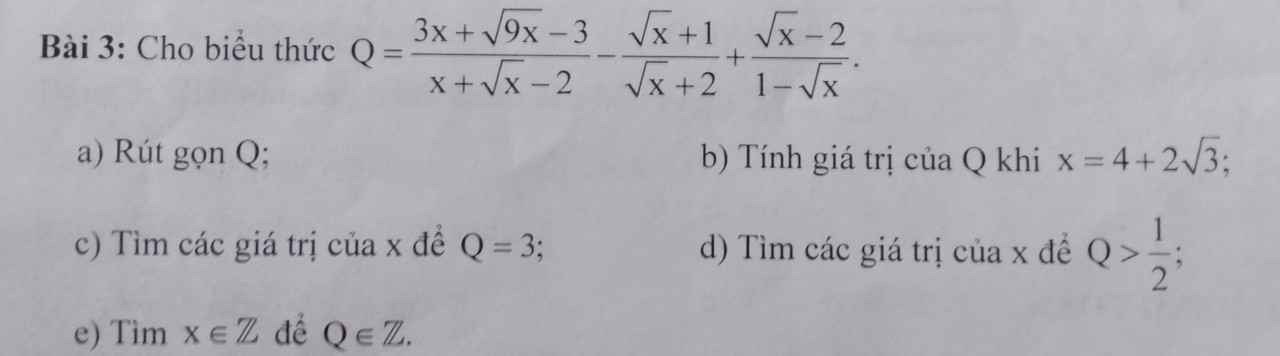 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp 


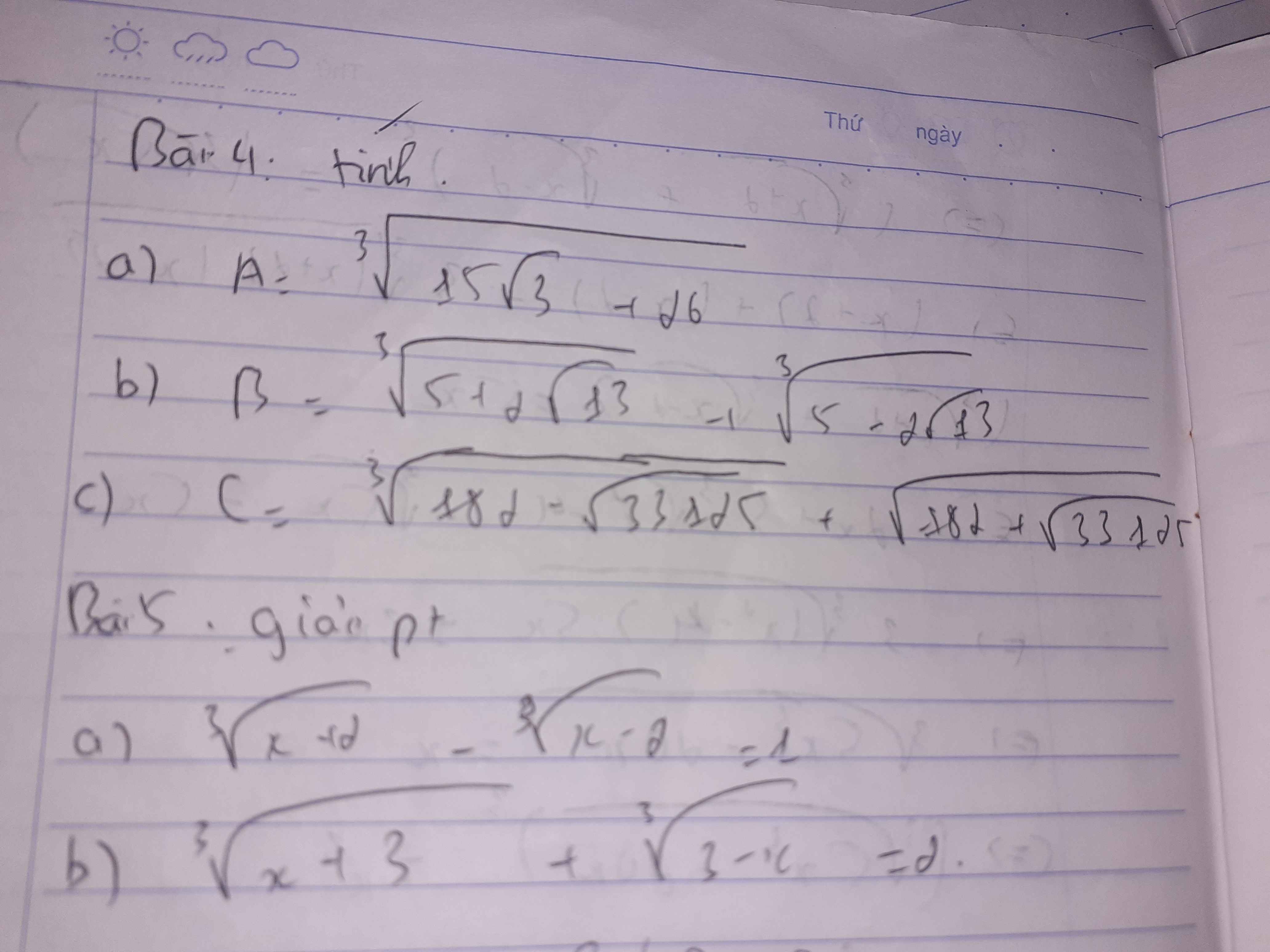
Câu 21:
1: \(\Leftrightarrow5\sqrt{x-1}=10\)
=>căn x-1=2
=>x-1=4
=>x=5
2: Để hai đường song song thì -2m=3m-5
=>-5m=-5
=>m=1