
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


PTHĐGĐ là:
1/2x^2-mx+2m+1=0
Δ=(-m)^2-4*1/2(2m+1)
=m^2-4m-2
Để (P) tiêp xúc (d) thì m^2-4m-2=0
=>\(m=2\pm\sqrt{6}\)
Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = mx - 2m - 1
⇔ x² = 2mx - 4m - 2
⇔ x² - 2mx + 4m + 2 = 0
Để (P) và (d) tiếp xúc thì phương trình hoành độ giao điểm của chúng có nghiệm kép
⇔ ∆´ = 0
⇔ m² - 4m - 2 = 0
∆´ = 4 + 2 = 6
m₁ = 2 + √6
m₂ = 2 - √6
Vậy m = 2 + √6; m = 2 - √6 thì (P) và (d) tiếp xúc


Câu 21:
1: \(\Leftrightarrow5\sqrt{x-1}=10\)
=>căn x-1=2
=>x-1=4
=>x=5
2: Để hai đường song song thì -2m=3m-5
=>-5m=-5
=>m=1

\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)

\(=\sqrt{3\left(x^2-2x+1\right)+25}\supseteq\sqrt{3\left(x+1\right)^2+25}\supseteq5\)
min=5 <=>x=-1
\(\text{Đặt }A=\sqrt{3x^2-6x+28}=\sqrt{3x^2-6x+3+25}\)
\(=\sqrt{3.\left(x^2-2x+1\right)+25}=\sqrt{3.\left(x-1\right)^2+25}\)
\(\Rightarrow A^2=3.\left(x-1\right)^2+25\ge25\Rightarrow A\ge\sqrt{25}=5\)
Dấu "=" xảy ra khi : x=1
Vậy GTNN của A là 5 tại x=1

a.
\(2x-x^2+7=-\left(x^2-2x+1\right)+8=-\left(x-1\right)^2+8\le8\)
\(\Rightarrow2+\sqrt{2x-x^2+7}\le2+\sqrt{8}=2+2\sqrt{2}\)
\(\Rightarrow\dfrac{3}{2+\sqrt{2x-x^2+7}}\ge\dfrac{3}{2+2\sqrt{2}}=\dfrac{3\sqrt{2}-3}{2}\)
\(A_{min}=\dfrac{3\sqrt{2}-3}{2}\) khi \(x=1\)
b. ĐKXĐ: \(x\le1\)
\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}-\dfrac{1}{2}-1\right)\)
\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}\right)+\dfrac{3}{2}\)
\(B=-\left(\sqrt{1-x}-\dfrac{\sqrt{2}}{2}\right)^2+\dfrac{3}{2}\le\dfrac{3}{2}\)
\(B_{max}=\dfrac{3}{2}\) khi\(x=\dfrac{1}{2}\)

Để pt có 2 nghiệm thì \(\Delta'=m^2-4\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\).
Khi đó theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4\end{matrix}\right.\).
Ta có \(\left(x_1+1\right)^2+\left(x_2+1\right)^2=2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=0\)
\(\Leftrightarrow\left(2m\right)^2-2.4+2.2m=0\Leftrightarrow m^2+m-2=0\Leftrightarrow\left(m-1\right)\left(m+2\right)=0\Leftrightarrow\left[{}\begin{matrix}m=1\left(l\right)\\m=-2\left(TM\right)\end{matrix}\right.\).
Vậy m = -2.

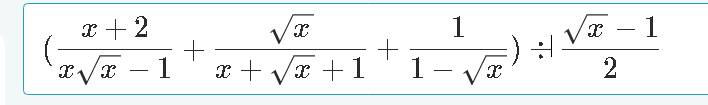 giúp mjk vs mjk đg cần gấp ạ
giúp mjk vs mjk đg cần gấp ạ
Đặt \(\frac{3m^2-2m+1}{\left(m+1\right)^2}=a\)\(\Leftrightarrow3m^2-2m-1=a\left(m+1\right)^2=am^2+2am+a\)
\(\Leftrightarrow3m^2-am^2-2m-2am+1-a=0\)
\(\Leftrightarrow\left(3-a\right)m^2-\left(2+2a\right)m+1-a=0\)
\(\Delta=\left(2+2a\right)^2-4\left(1-a\right)\left(3-a\right)=24a-8\)
Để pt có nghiệm:\(24a-8\ge0\Leftrightarrow a\ge\frac{1}{3}\)
Vậy bt ban đầu đạt GTNN là 1/3 khi m=1/2
Đọc tự hiểu nhé ,có j kb hỏi lại mik