
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì xy = 1
Suy ra : x , y thuộc Ư(1) = {-1;1}
+ x = -1 và y = -1 thì GTNN của |x + y| = 0
+ x = 1 và y = 1 thì GTNN của |x + y| = 2
Vậy GTNN của |x + y| = 0

Bài 3:
a: Ta có: \(x^2+5x+5xy+25y\)
\(=x\left(x+5\right)+5y\left(x+5\right)\)
\(=\left(x+5\right)\left(x+5y\right)\)
b: Ta có: \(x^2-y^2+14x+49\)
\(=\left(x+7\right)^2-y^2\)
\(=\left(x+7-y\right)\left(x+7+y\right)\)

a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27

XXét tứ giác AMDN có ^AMD=^MAN=^AND=90∞
⇒AMDN là hình chữ nhật
hcn AMDN có AD là phân giác góc A
⇒AMDN là hình vuông(dấu hiệu 3)

Ta có : \(\left(3x-2\right)\left(4x+3\right)=\left(2-3x\right)\left(x-1\right)\)
\(\Leftrightarrow12x^2-8x+9x-6=2x-3x^2-2+3x\)
\(\Leftrightarrow12x^2-8x+9x-6-2x+3x^2+2-3x=0\)
\(\Leftrightarrow15x^2-4x-4=0\)
\(\Leftrightarrow15x^2-10x+6x-4=0\)
Lỗi :vvvv
\(\Leftrightarrow10x\left(\dfrac{3}{2}x-1\right)+4\left(\dfrac{3}{2}x-1\right)=0\)
\(\Leftrightarrow\left(10x+4\right)\left(\dfrac{3}{2}x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{5}\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy ...

\(x^2-6x+8\)
\(C1\) \(=x^2-4x-2x+8\)
\(=\left(x^2-4x\right)-\left(2x-8\right)\)
\(=x\left(x-4\right)-2\left(x-4\right)\)
\(=\left(x-2\right)\left(x-4\right)\)
\(C2\): \(x^2-6x+8\)
\(=x^2-6x+9-1\)
\(=\left(x^2-6x+9\right)-1\)
\(=\left(x-3\right)^2-1\)
\(=\left(x-3-1\right)\left(x-3+1\right)\)
\(=\left(x-4\right)\left(x-2\right)\)
\(C3\) \(x^2-6x+8\)
\(=x^2-2x-4x+8\)
\(=\left(x^2-2x\right)-\left(4x-8\right)\)
\(=x\left(x-2\right)-4\left(x-2\right)\)
\(=\left(x-2\right)\left(x-4\right)\)

3x(x-1)=1-x
<=> 3x(x-1) +x-1=0
<=> (x-1)(3x+1)=0
\(\Rightarrow\orbr{\begin{cases}x-1=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{1}{3}\end{cases}}}\)
Vậy...

a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)



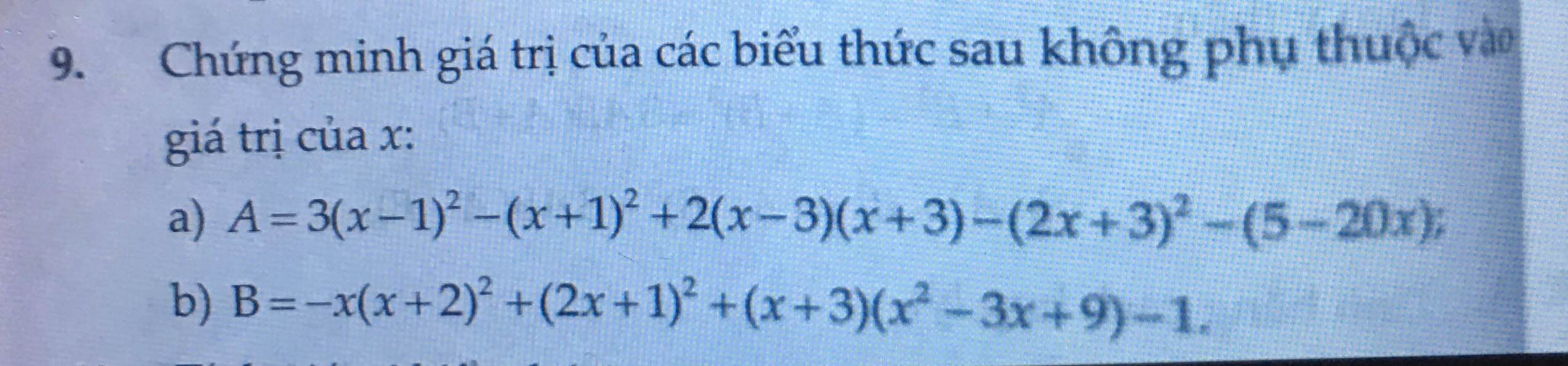

 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Bài 5:
a: \(M=\dfrac{x-1}{2}:\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)}{2}\cdot\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}\)
\(=\dfrac{x^3-1}{2x}\)
bạn trả lời lúc 12 giờ