K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
21 tháng 12 2021
Để 2 hàm số cắt nhau tại 1 điểm trên trục tung thì:
y1= 2x1+m-3=y2=5x2+5-3m và x1=x2=0
=> m-3=5-3m
<=> 4m=8
<=>m=2
N
27 tháng 11 2021
\(M\left(2;6\right)\in y=ax+5\Leftrightarrow6=a\cdot2+5\Rightarrow a=\dfrac{1}{2}\)
N
1
27 tháng 10 2021
Bài 4:
a) áp dụng pi-ta-go ta có:\(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{15^2+20^2}=25\)
áp dụng HTL ta có: \(AB.AC=BC.AH\Rightarrow\dfrac{15.20}{25}=AH\Rightarrow AH=12\)
b) áp dụng HTL và ΔAHB ta có: \(AI.AB=AH^2\)
áp dụng HTL và ΔAHC ta có: \(AJ.AC=AH^2\)
\(\Rightarrow AI.AB=AJ.AC\)
N
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
6.B
Hàm nghịch biến trên R khi:
\(1-m< 0\Rightarrow m>1\)
5.B
Đồ thị đi qua A nên:
\(-1=2a-2\Rightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)
22 tháng 9 2021
\(ĐK:x\in R\\ PT\Leftrightarrow\sqrt{\left(x+\dfrac{1}{2}\right)^2}=7-2x\\ \Leftrightarrow\left|x+\dfrac{1}{2}\right|=7-2x\\ \Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=7-2x,\forall x+\dfrac{1}{2}\ge0\\x+\dfrac{1}{2}=2x-7,\forall x+\dfrac{1}{2}< 0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13}{6},\forall x\ge-\dfrac{1}{2}\left(tm\right)\\x=\dfrac{15}{2},\forall x< -\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{13}{6}\)
1 tháng 9 2021
a)\(MinA=1\Leftrightarrow x=\dfrac{1}{4}\)
b)\(MaxP=1\Leftrightarrow x=\dfrac{1}{4}\)
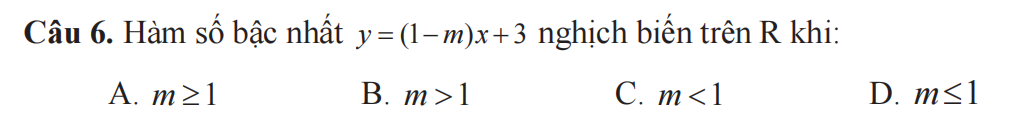
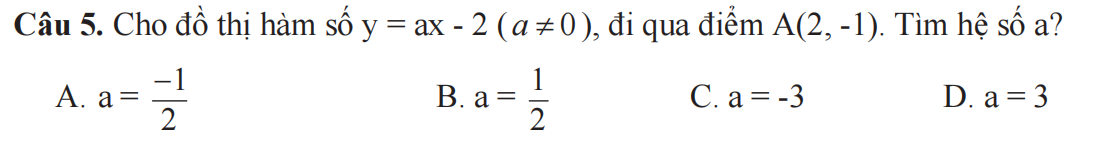
1)Thay x=4 vào biểu thức B ta được:
\(B=\left(\dfrac{x+1}{2}-\sqrt{x}\right)=\left(\dfrac{4+1}{2}-\sqrt{4}\right)=\dfrac{1}{2}\)
2)\(M=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right)\left(\dfrac{x+1}{2}-\sqrt{x}\right)\) (đk:\(x\ge0;x\ne1\))
\(=\dfrac{\sqrt{x}+1-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x+1-2\sqrt{x}}{2}\)
\(=\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
3) \(M=\dfrac{\sqrt{x}}{6}\)
=> \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}}{6}\) \(\Leftrightarrow6\left(\sqrt{x}-1\right)=\sqrt{x}\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow x-5\sqrt{x}+6=0\) \(\Leftrightarrow\)\(\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=4\end{matrix}\right.\) (thỏa)
Vậy...
a) \(x=4\rightarrow\sqrt{x}=2\) (TMĐK)
Thay \(\sqrt{x}=2\) vào A ta có :
\(A=\left(\dfrac{1}{2-1}-\dfrac{1}{2+1}\right)=\left(1-\dfrac{1}{3}\right)=\dfrac{2}{3}\)
b) M=A.B
\(\rightarrow M=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right).\left(\dfrac{x+1}{2}-\sqrt{x}\right)\)
\(\rightarrow M=\left(\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\left(\dfrac{x+1-2\sqrt{x}}{2\sqrt{x}}\right)\)
\(\rightarrow M=\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{2\sqrt{x}}\)
\(\rightarrow M=\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(M=\dfrac{\sqrt{x}}{6}\)
\(\rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{6}\)
\(\rightarrow6\left(\sqrt{x}-1\right)=\sqrt{x}+1\)
\(\rightarrow6\sqrt{x}-6-\sqrt{x}-1=0\)
\(\rightarrow5\sqrt{x}-7=0\)
\(\rightarrow\sqrt{x}=\dfrac{7}{5}\)
\(\rightarrow x=\pm\dfrac{5\sqrt{7}}{5}\)
\(\rightarrow x=\dfrac{5\sqrt{7}}{7}\) (TMĐK)