K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
VT
0
23 tháng 8 2021
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC
Suy ra: \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
hay \(AC^2=HC\cdot BC\)
c: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
Suy ra: \(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
hay \(AH^2=HB\cdot HC\)
27 tháng 5 2022
\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
92
0
13 tháng 2 2022
a,\(\Delta=3^2-4\left(-2\right).6=9+48=57\)
\(x_1=\dfrac{-3+\sqrt{57}}{-4}=\dfrac{3-\sqrt{57}}{4}\)
\(x_2=\dfrac{-3-\sqrt{57}}{-4}=\dfrac{3+\sqrt{57}}{4}\)
b, \(\Delta=6^2-4.3.3=36-36=0\)
\(\Rightarrow x_1=x_2=\dfrac{-6}{2.3}=\dfrac{-6}{6}=-1\)
c, \(\Delta=1^2-4.6.5=1-120=-119< 0\)
Vậy pt vô nghiệm
2
27 tháng 5 2022
`48/[x+4]+48/[x-4]=5` `ĐK: x \ne +-4`
`<=>[48(x-4)+48(x+4)]/[(x-4)(x+4)]=[5(x+4)(x-4)]/[(x-4)(x+4)]`
`=>48x-192+48x+192=5x^2-80`
`<=>5x^2-96x-80=0`
`<=>5x^2-100+4x-80=0`
`<=>5x(x-20)+4(x-20)=0`
`<=>(x-20)(5x+4)=0`
`<=>` $\left[\begin{matrix} x=20\\ x=\dfrac{-4}{5}\end{matrix}\right.$ (t/m)
Vậy `S={-4/5;20}`
TC
27 tháng 5 2022
ĐK : \(x\ne\pm4\)
\(\Leftrightarrow\cdot\dfrac{48\left(x+4\right)+48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow48x+192+48x-192==5x^2-80\)
\(\Leftrightarrow96x=5x^2-80\)
\(\Leftrightarrow5x^2-96x-80=0\)
\(\Leftrightarrow5x^2+4x-100-80=0\)
\(\Leftrightarrow4\left(x-20\right)+5x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\5x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-\dfrac{4}{5}\end{matrix}\right.\)
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
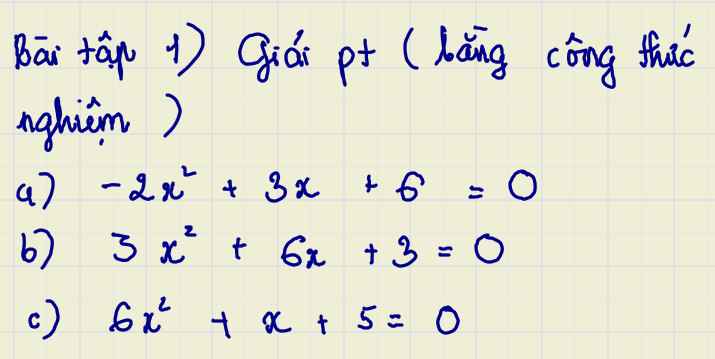
a)\(MinA=1\Leftrightarrow x=\dfrac{1}{4}\)
b)\(MaxP=1\Leftrightarrow x=\dfrac{1}{4}\)
giải chi tiết mà