
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)


a, -5/11.7/15.(11/-5)(-30)
=(-5/11.11/-5).(7/15.-30)
=1.7.(-30)/15
=1.7.(-2).15/15
=1.7.(-2)
=-14
b,(11/12):(33/36).3/5
=11/12:(11.3/12.3).3/5
=11/12:11/12.3/5
=1.3/5
=3/5
c,(-5/-9).3/11+(-13/18).3/11
=5/9.3/11+ -13/18.3/11
=3/11.(5/9+ -13/18)
=3/11.(10/18+ -13/18)
=3/11.-3/18
= -9/198
= -1/22
Bài 2:
a,-7/15.5/8.15/7.(-16)
=(-7/15.15/7)(5/8. -16)
= -1.-10
= 10
b,(-1/-2).16/5+(-1/-2)(-11/5)
= 1/2.16/5+1/2. (-11/5)
=1/2.(16/5+ -11/5)
=1/2.5/5
=1/2.1
=1/2
học tốt nha bạn. chúc bạn thành công

b: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
\(=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}\)
\(=k^2\)(1)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}\)
\(=\dfrac{\left(bk\right)^2-\left(dk\right)^2}{b^2-d^2}\)
\(=k^2\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{a^2-c^2}{b^2-d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4bk+3dk}{4b+3d}=k\)
\(\dfrac{4a-3c}{4b-3d}=\dfrac{4bk-3dk}{4b-3d}=k\)
Do đó: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4a-3c}{4b-3d}\)
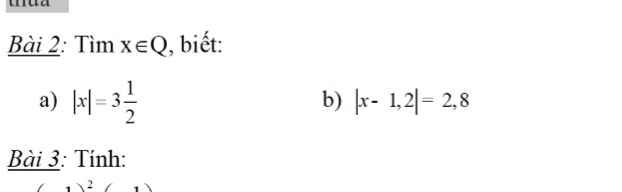
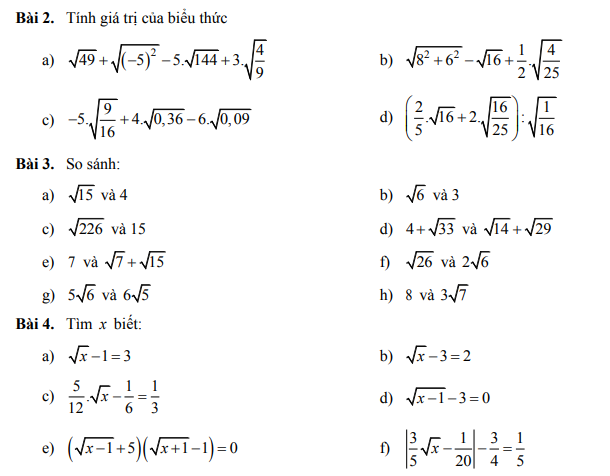 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy


a) \(\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow\left|x\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
b) \(\left|x-1,2\right|=2,8\)
\(\Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1,6\end{matrix}\right.\)
\(a,\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow x=\left[{}\begin{matrix}3\dfrac{1}{2}\\-3\dfrac{1}{2}\end{matrix}\right.\)
\(b,\left|x-1,2\right|=2,8\\ \Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2,8+1,2=4\\x=-2,8+1,2=-1,6\end{matrix}\right.\)
Vậy \(x\in\left\{4;-1,6\right\}\)