NL
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 10 2021
a) \(\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow\left|x\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
b) \(\left|x-1,2\right|=2,8\)
\(\Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1,6\end{matrix}\right.\)
H
4 tháng 10 2021
\(a,\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow x=\left[{}\begin{matrix}3\dfrac{1}{2}\\-3\dfrac{1}{2}\end{matrix}\right.\)
\(b,\left|x-1,2\right|=2,8\\ \Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2,8+1,2=4\\x=-2,8+1,2=-1,6\end{matrix}\right.\)
Vậy \(x\in\left\{4;-1,6\right\}\)
4 tháng 9 2021
b: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
\(=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}\)
\(=k^2\)(1)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}\)
\(=\dfrac{\left(bk\right)^2-\left(dk\right)^2}{b^2-d^2}\)
\(=k^2\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{a^2-c^2}{b^2-d^2}\)
4 tháng 9 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4bk+3dk}{4b+3d}=k\)
\(\dfrac{4a-3c}{4b-3d}=\dfrac{4bk-3dk}{4b-3d}=k\)
Do đó: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4a-3c}{4b-3d}\)
20 tháng 9 2016
Bạn xem lại đề:
bài 1:
hình như sai đề, phải là 2,4; 4,9; 2,1; 5,6
Bài 2:
Hình như là \(7\frac{1}{3}\) đó
21 tháng 12 2021
Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
DT
9 tháng 2 2022
bài này ko cần pytago cx đc:
Ta có:
CB=CD
=> FB<CD ( F nằm trên đường thẳng CB)(1)
theo đề suy ra được : tam giác EFD nằm trong tam giác EBD
<=>FD<CB ( vì FD là cạnh nằm trong tam giác và tiếp với đường cao tam giác ngoài)(2)
Từ (1) và (2) suy ra : CD+CB>FD+FB( đpcm)
30 tháng 9 2021
Bài 6:
a: \(C=-\left|2x-5\right|+3\le3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
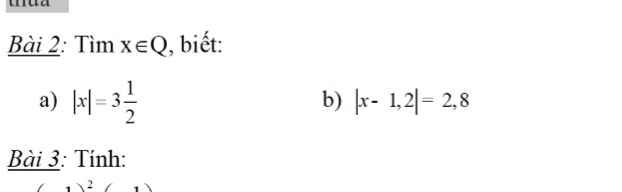
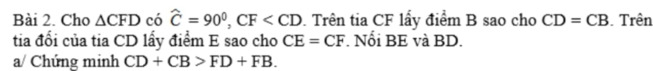
Cái gì vậy chơi bài có qué mà chị cho em kết bạn nhé
oki em