K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 6 2023
3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM
CA
1
8 tháng 8 2021
12.
a)
\(P=\dfrac{\sqrt{x}-1+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\left(x>0;x\ne1\right)\\ P=\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\dfrac{1}{\sqrt{x}}\)
28 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }-x-7=-3x+1\Leftrightarrow x=4\Leftrightarrow y=-11\Leftrightarrow B\left(4;-11\right)\\ c,\text{Gọi }\left(D_3\right):y=ax+b\left(a\ne0\right)\\ \left(D_3\right)\text{//}\left(D_1\right)\Leftrightarrow a=-1;b\ne-7\Leftrightarrow\left(D_3\right):y=-x+b\\ \left(D_3\right)\cap\left(D_2\right)\text{tại điểm có tung độ }4\Leftrightarrow\left\{{}\begin{matrix}4=-3x+1\\4=-x+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\b=3\end{matrix}\right.\\ \text{Vậy }\left(D_3\right):y=-x+3\)
\(d,\Leftrightarrow B\left(4;-11\right)\in\left(D_4\right)\\ \Leftrightarrow8m-4-5m-2=-11\\ \Leftrightarrow3m=-5\Leftrightarrow m=-\dfrac{5}{3}\\ e,\Leftrightarrow\left\{{}\begin{matrix}-x-7=0\\\left(2m-1\right)x-5m-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-7\\7-14m-5m-2=0\end{matrix}\right.\\ \Leftrightarrow m=\dfrac{5}{19}\)
20 tháng 8 2021
Lần sau đăng tách bài ra bạn nhé.
Câu 8
Câu 1, ý a và b:
20 tháng 8 2021
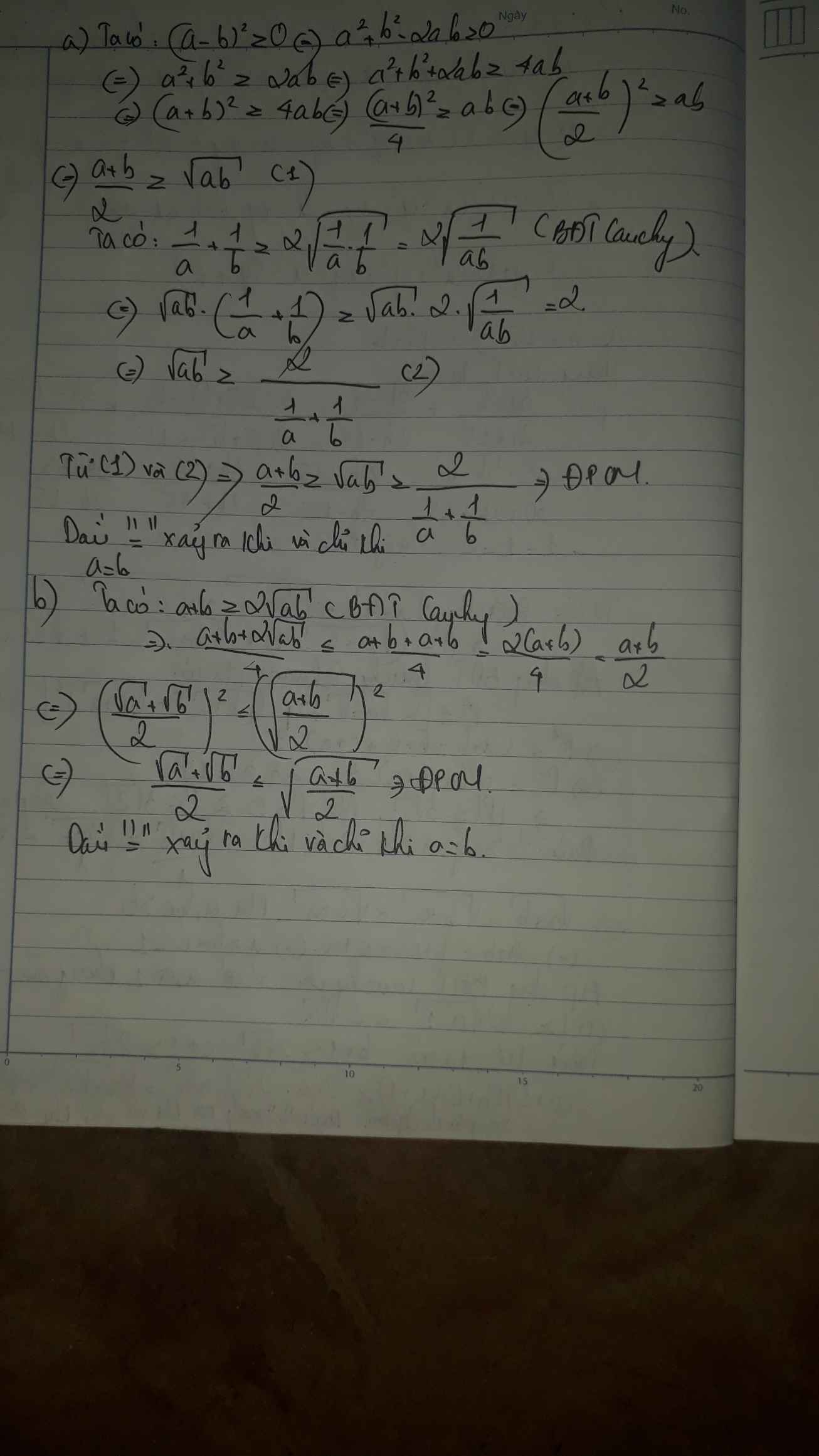
Câu 7:
Ta có: \(\dfrac{x}{\sqrt{4x-1}}\ge\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{2x-\sqrt{4x-1}}{2\sqrt{4x-1}}\ge0\)
\(\Leftrightarrow2x-\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-2\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-1-2\cdot\sqrt{4x-1}\cdot1+1\ge0\)
\(\Leftrightarrow\left(\sqrt{4x-1}-1\right)^2\ge0\forall x\) thỏa mãn ĐKXĐ
