K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
8 tháng 1 2022
Bài 6:
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔADM và ΔAEM có
AD=AE
\(\widehat{DAM}=\widehat{EAM}\)
AM chung
Do đó: ΔADM=ΔAEM
Suy ra: \(\widehat{ADM}=\widehat{AEM}=90^0\)
hay ME⊥AC
HN
1
3 tháng 3 2022
a: \(=\dfrac{-1}{3}\cdot\dfrac{3}{2}x^2y\cdot xy^3=-\dfrac{1}{2}x^3y^4\)
b: \(=\left(-5\right)\cdot\left(-0.2\right)\cdot xy^4\cdot x^2y^2=x^3y^6\)
c: \(=-2\cdot5\cdot x^2y\cdot x^3y^3=-10x^5y^4\)
d: \(=\left(-\dfrac{3}{2}x^2y^3\right)^2=\dfrac{9}{4}x^4y^6\)
8 tháng 3 2022
a) Xét \(\Delta ABC:\)
\(BC^2=10^2=100\left(cm\right).\\ AB^2+AC^2=6^2+8^2=100\left(cm\right).\\ \Rightarrow AB^2+AC^2=BC^2.\)
\(\Rightarrow\Delta ABC\) vuông tại A.
b) M là trung điểm AB (gt).
\(\Rightarrow AM=BM=\dfrac{1}{2}AB=\dfrac{1}{2}6=3\left(cm\right).\)
Xét \(\Delta AMC\) vuông tại A:
\(CM^2=AM^2+AC^2\left(Pytago\right).\\ \Rightarrow CM^2=3^2+8^2.\\ \Rightarrow CM=\sqrt{73}\left(cm\right).\)
c) BD // AC (gt).
\(\Rightarrow\widehat{MAC}=\widehat{MBD}=90^o\left(Soletrong\right).\)
Xét \(\Delta MAC\) và \(\Delta MBD:\)
\(\widehat{AMC}=\widehat{BMD}\) (đối đỉnh).
\(\widehat{MAC}=\widehat{MBD}\left(cmt\right).\\ AM=BM\left(cmt\right).\)
\(\Rightarrow\Delta MAC=\Delta MBD\left(g-c-g\right).\)
\(\Rightarrow AC=BD\) (2 cạnh tương ứng).
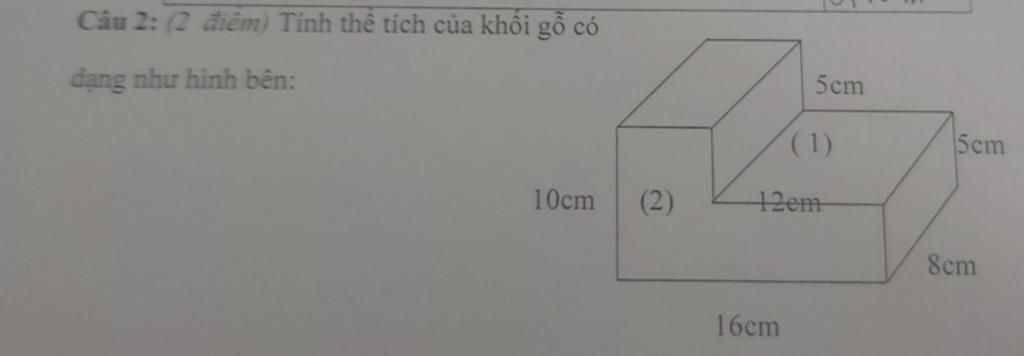
(16x8x10)-(12x8x5)=800cm3