
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(A=2x^2-6x=2\left(x^2-3x\right)=2\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Suy ra Min A = -9/2 <=> x = 3/2
Ta có : \(A=2x^2-6x\)
\(=2\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)
Có : \(2\left(x-\frac{3}{2}\right)^2\ge0\)
\(\Rightarrow2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Dấu " = " xảy ra khi và chỉ khi \(x-\frac{3}{2}=0\)
\(\Leftrightarrow x=\frac{3}{2}\)
Vậy \(Min_A=\frac{-9}{2}\) khi và chỉ khi \(x=\frac{3}{2}\)

Đặt x^2 + 2x = a ta có:
a^2 - 9a + 20 = (a - 4)(a - 5)
Thay ngược lại ta có: (x^2 + 2x - 4)(x^2 + 2x - 5)

Với a,b >0.Ta có: \(\frac{1}{a}+\frac{1}{b}\ge\frac{\left(1+1\right)^2}{a+b}=\frac{4}{a+b}\left(đpcm\right)\)
Dấu = xảy ra khi và chỉ khi a=b

Rút gọn :
b ) \(\frac{x^2+3xy+2y^2}{x^2+2x^2y-xy^2-2y^2}\)
\(=\frac{x^2+xy+2xy+2y^2}{x^3-xy^2+2x^2y-2y^3}\)
\(=\frac{x\left(x+4\right)+2y\left(x+y\right)}{x\left(x^2-y^2\right)+2y\left(x^2-y^2\right)}\)
\(=\frac{\left(x+y\right)\left(x+2y\right)}{\left(x^2-y^2\right)\left(x+2y\right)}\)
\(=\frac{\left(x+y\right)\left(x+2y\right)}{\left(x-y\right)\left(x+y\right)\left(x+2y\right)}\)
\(=\frac{1}{x-y}\)

a, Độ dài mặt cầu trượt là \(\dfrac{2,1}{\sin28^0}\approx4,5\left(m\right)\)
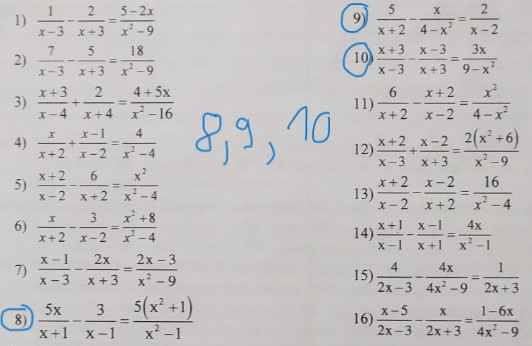 Giup mình bài 8,9,10
Giup mình bài 8,9,10


8: =>5x(x-1)-3(x+1)=5x^2+5
=>5x^2-5x-3x-3=5x^2+5
=>-8x=8
=>x=-1(loại)
9: =>5(x-2)+x=2(x+2)
=>5x-10+x=2x+4
=>6x-10=2x+4
=>4x=14
=>x=3,5(nhận)
10: =>(x+3)^2-(x-3)^2=-3x
=>x^2+6x+9-x^2+6x-9=-3x
=>12x+3x=0
=>x=0
\(8,\dfrac{5x}{x+1}-\dfrac{3}{x-1}=\dfrac{5\left(x^2+1\right)}{x^2-1}\left(dkxd:x\ne\pm1\right)\)
\(\Leftrightarrow\dfrac{5x}{x+1}-\dfrac{3}{x-1}-\dfrac{5\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow5x\left(x-1\right)-3\left(x+1\right)-5x^2-5=0\)
\(\Leftrightarrow5x^2-5x-3x-3-5x^2-5=0\)
\(\Leftrightarrow-8x-8=0\)
\(\Leftrightarrow-8\left(x+1\right)=0\)
\(\Leftrightarrow x=-1\left(ktmdk\right)\)
Vậy \(S=\varnothing\)
\(9,\dfrac{5}{x+2}-\dfrac{4}{4-x^2}=\dfrac{2}{x-2}\)
\(\Leftrightarrow\dfrac{5}{x+2}-\dfrac{4}{x^2-4}-\dfrac{2}{x-2}=0\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow5\left(x-2\right)-4-2\left(x+2\right)=0\)
\(\Leftrightarrow5x-10-4-2x-4=0\)
\(\Leftrightarrow3x-18=0\)
\(\Leftrightarrow3x=18\)
\(\Leftrightarrow x=6\left(tmdk\right)\)
Vậy \(S=\left\{6\right\}\)