
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)

Gọi thời gian của T,D,M lần lượt là \(a,b,c(giờ;a,b,c>0)\)
Áp dụng tc dtsbn:
\(10a=9b=8c\Leftrightarrow\dfrac{10a}{360}=\dfrac{9b}{360}=\dfrac{8c}{360}\Leftrightarrow\dfrac{a}{36}=\dfrac{b}{40}=\dfrac{c}{45}=\dfrac{c-a}{45-36}=\dfrac{0,3}{9}=\dfrac{1}{30}\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{6}{5}\\b=\dfrac{4}{3}\\c=\dfrac{3}{2}\end{matrix}\right.\)
Vậy ...

\(\text{Bài 1:a)}25\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)-35\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\dfrac{478}{19}.\left(-\dfrac{4}{5}\right)-\dfrac{668}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{478}{19}-\dfrac{668}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{-190}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(-10\right)=8\)
\(\text{b)}5:\left(-\dfrac{5}{2}\right)^2+\dfrac{2}{15}.\sqrt{\dfrac{9}{4}}-\left(-2021\right)^0+0,25\)
\(=5:\dfrac{25}{4}+\dfrac{2}{15}.\dfrac{3}{2}-1+\dfrac{1}{4}\)
\(=\dfrac{4}{5}+\dfrac{1}{5}-1+\dfrac{1}{4}\)
\(=1-1+\dfrac{1}{4}\)
\(=0+\dfrac{1}{4}=\dfrac{1}{4}\)
\(\text{Bài 2:a)}\dfrac{8}{5}-\dfrac{3}{5}:x=0,4\)
\(\dfrac{3}{5}:x=\dfrac{8}{5}-0,4=\dfrac{6}{5}\)
\(x=\dfrac{3}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\text{b)}\left(3x-\dfrac{1}{2}\right)^2+\dfrac{21}{25}=1\)
\(\left(3x-\dfrac{1}{2}\right)^2\) \(=1-\dfrac{21}{25}=\dfrac{4}{25}=\pm\left(\dfrac{2}{5}\right)^2\)
\(\text{Vậy }3x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(3x\) \(=\dfrac{2}{5}+\dfrac{1}{2}=\dfrac{9}{10}\)
\(x\) \(=\dfrac{9}{10}.\dfrac{1}{3}=\dfrac{3}{10}\)
\(\text{hoặc }3x-\dfrac{1}{2}=\dfrac{-2}{5}\)
\(3x\) \(=\left(\dfrac{-2}{5}\right)+\dfrac{1}{2}=\dfrac{1}{10}\)
\(x\) \(=\dfrac{1}{10}.\dfrac{1}{3}=\dfrac{1}{30}\)
\(\Rightarrow x\in\left\{\dfrac{3}{10};\dfrac{1}{30}\right\}\)
Bài 2:
a: =>3/5:x=6/5
hay x=3/5:6/5=1/2
b: \(\Leftrightarrow\left(3x-\dfrac{1}{2}\right)^2=\dfrac{4}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{1}{2}=\dfrac{2}{5}\\3x-\dfrac{1}{2}=-\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{10}\\x=\dfrac{1}{30}\end{matrix}\right.\)

\(a,\Leftrightarrow m-2=3\Leftrightarrow m=5\\ b,y=f\left(x\right)=\left(5-2\right)x=3x\\ \Leftrightarrow f\left(3\right)+\dfrac{1}{3}f\left(-2\right)=9+\dfrac{1}{3}\cdot\left(-6\right)=7\)

Bài 4:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD

Bài 11:
a) Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBAD=ΔBED(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(đpcm)

 mn giúp mik vs mik cần gấp( có trình bày nha~)
mn giúp mik vs mik cần gấp( có trình bày nha~)
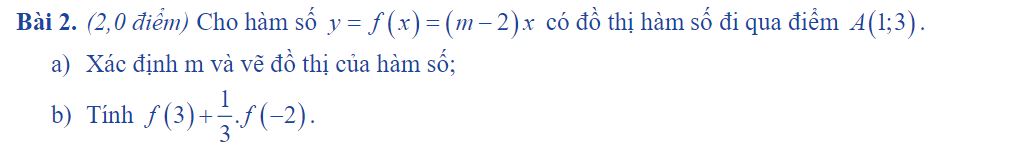 mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)
mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)

a) 3,2x+(-1,2)x+2,7=-4,9
⇔(3,2-1,2)x+2,7=-4,9
⇔2x=-7,6
⇔x=-3,8
Vậy x=-3,8
b)(-5,6)x+2,9x-3,86=-9,8
⇔(2,9-5,6)x-3,86=-9,8
⇔-2,7x=-5,94
⇔x=2,2
Vậy x=2,2
cảm ơn bạn