K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 9 2021
\(\dfrac{x}{6}=\dfrac{7}{4}\Rightarrow x=\dfrac{6\cdot7}{4}=\dfrac{21}{2}\\ \dfrac{3}{x}=\dfrac{21}{17}\Rightarrow x=\dfrac{3\cdot17}{21}=\dfrac{17}{7}\)
4 tháng 2 2022
Bài 19:
a: \(A=5x+\dfrac{1}{9}y=5\cdot\dfrac{-1}{10}+\dfrac{1}{9}\cdot4.8=\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(A=x-\dfrac{2}{3}=\dfrac{-1}{3}-\dfrac{2}{3}=-1\)
4 tháng 2 2022
\(a,7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+\dfrac{1}{9}y\\ =5.\left(\dfrac{-1}{10}\right)+\dfrac{1}{9}.4,8\\ =\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{1}{30}\\ b,x=\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{-7}{40}+\dfrac{5}{11}}{\dfrac{21}{80}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{123}{440}}{\dfrac{-369}{880}}=\dfrac{-1}{3}+\dfrac{-2}{3}=\dfrac{-3}{3}=\left(-1\right)\)
14 tháng 7 2021
Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)
26 tháng 9 2021
\(8,\\ b,4^{333}=\left(4^3\right)^{111}=64^{111}< 81^{111}=\left(3^4\right)^{111}=3^{444}\\ c,2^{500}=\left(2^5\right)^{100}=32^{100}>25^{100}=\left(5^2\right)^{100}=5^{200}\\ d,2^{375}=\left(2^3\right)^{125}=8^{125}< 9^{125}=\left(3^2\right)^{125}=3^{250}\)
26 tháng 9 2021
b: \(4^{333}=\left(4^3\right)^{111}=64^{111}\)
\(3^{444}=\left(3^4\right)^{111}=81^{111}\)
mà 64<81
nên \(4^{333}< 3^{444}\)
c: \(2^{500}=\left(2^5\right)^{100}=32^{100}\)
\(5^{200}=\left(5^2\right)^{100}=25^{100}\)
mà 32>25
nên \(2^{500}>5^{200}\)
29 tháng 7 2019
a) Ta có: 2|x + 2| \(\ge\)0 \(\forall\)x
=> 2|x + 2| + 15 \(\ge\)15 \(\forall\)x
Hay A \(\ge\)15 \(\forall\)x
Dấu "=" xảy ra <=>x + 2 = 0 <=> x = -2
Vậy Min A = 15 tại x = -2
b) Ta có: 2(x + 5)4 \(\ge\)0 \(\forall\)x
3|x + y + 2| \(\ge\)0 \(\forall\)x;y
=> 20 - 2(x + 5)4 - 3|x + y + 2| \(\le\)20 \(\forall\)x;y
Hay B \(\le\)20 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+5=0\\x+y+2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=-5\\y=-2-x\end{cases}}\) <=> \(\hept{\begin{cases}x=-5\\y=-2-\left(-5\right)=3\end{cases}}\)
Vậy Max B = 20 tại x = -5 và y = 3
16 tháng 9 2021
\(a,\left\{{}\begin{matrix}Az\perp Ox\\Ox\perp Oy\left(\widehat{xOy}=90^0\right)\end{matrix}\right.\Rightarrow Az//Oy\)
\(b,\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \widehat{nAx}=\dfrac{1}{2}\widehat{xAz}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \Rightarrow\widehat{xOm}=\widehat{nAx}\left(=45^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(Om//An\)
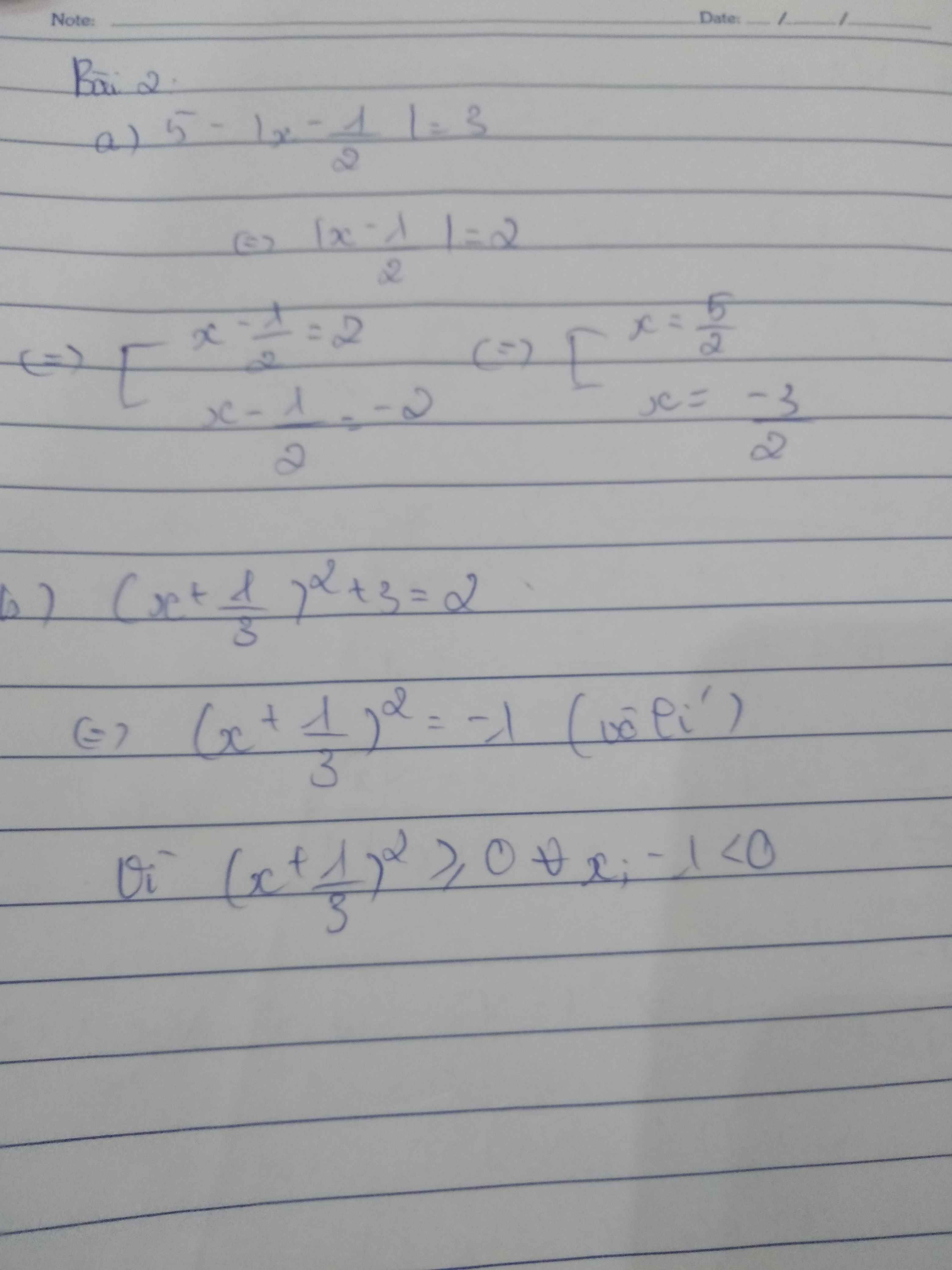
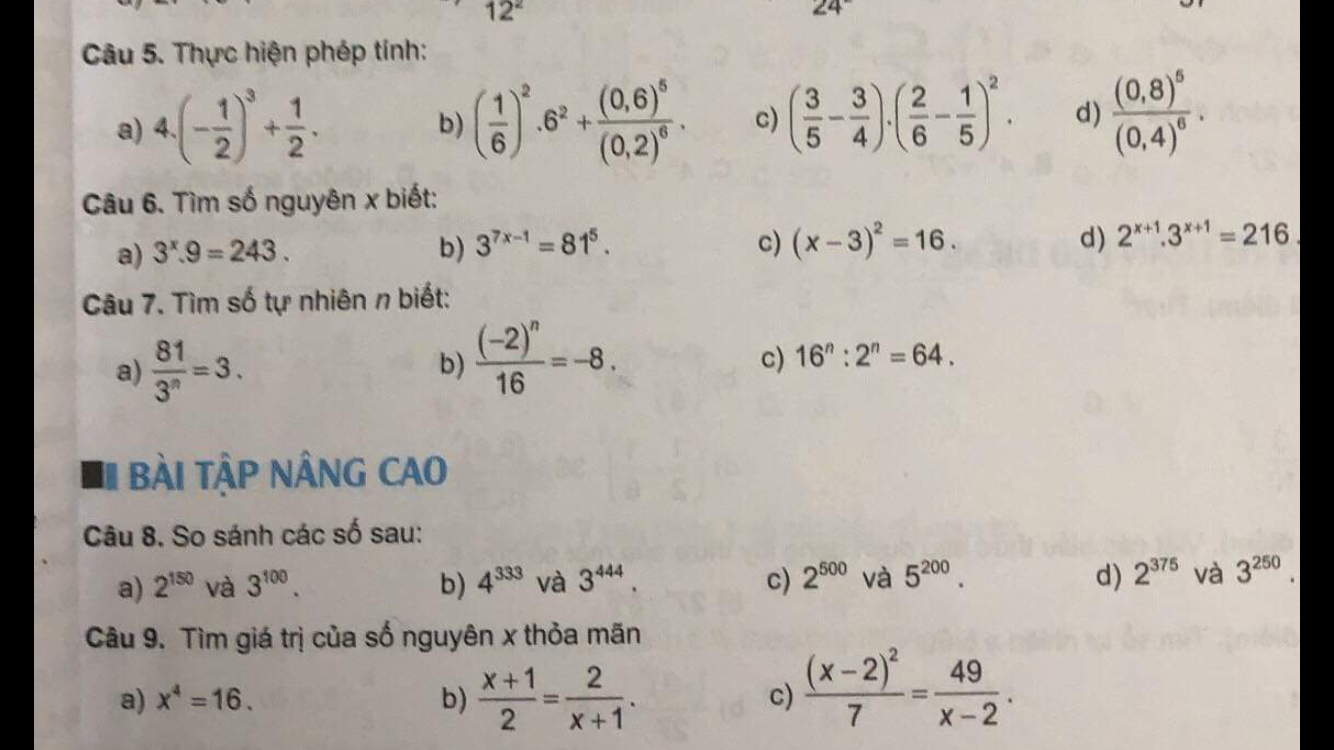
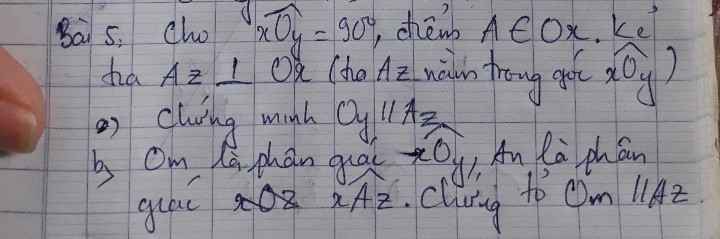
Câu 2:
1.Do xy\(\perp\)CD mà zt\(\perp\)CD
\(=>xy//zt\)
2.\(=>\widehat{ABt}=\widehat{mAy}=46\left(haigocdongvi\right)\)