
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(M=\left(\dfrac{x+3}{x-3}-\dfrac{18}{\left(x-3\right)\left(x+3\right)}+\dfrac{x-3}{x+3}\right):\dfrac{x+3-x-1}{x+3}\)
\(=\dfrac{x^2+6x+9-18+x^2-6x+9}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{2}\)
\(=\dfrac{2x^2}{x-3}\cdot\dfrac{1}{2}=\dfrac{x^2}{x-3}\)
b: Để M nguyên thì \(x^2-9+9⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{4;2;6;0;12;-6\right\}\)

b1:
AMF đồng dạng ABC
tỉ số : AM/AF = AB/AC
AM/MF = AB/BC
AF/FM = AC/CB
MFD đồng dạng CFD
tỉ số : MF/FD= FD/DC
FM/MD = DC/CF
FD/DM = DF/FC
AFB đồng dạng CFB
tỉ số : AB/ BF = BF/FC
AF/AB =BF/ BC
AF / FB = CF/BC

bạn đăng tách ra nhé
Bài 3 :
Ta có :\(1+\dfrac{1}{2+x}=\dfrac{12}{x^3+8}\)
đk : x khác -2
\(\Rightarrow x^3+8+x^2-2x+4=12\Leftrightarrow x^3+x^2-2x=0\)
\(\Leftrightarrow x\left(x^2+x-2\right)=0\Leftrightarrow x\left(x-1\right)\left(x+2\right)=0\Leftrightarrow x=0;x=1;x=-2\left(ktm\right)\)
Bài 2:
a,ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(\dfrac{1}{x}+\dfrac{2}{x-2}=0\\ \Leftrightarrow\dfrac{x-2}{x\left(x-2\right)}+\dfrac{2x}{x\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x-2+2x}{x\left(x-2\right)}=0\\ \Rightarrow3x-2=0\\ \Leftrightarrow x=\dfrac{2}{3}\left(tm\right)\)
b, ĐKXĐ:\(x\ne\pm2\)
\(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{5x-2}{4-x^2}\\ \Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2-5x}{x^2-4}\\ \Leftrightarrow\dfrac{x^2-3x+2-x^2-2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2-5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow\dfrac{-5x+2-2+5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow0=0\left(tm\right)\)


a) Xét ΔBAC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
Xét tứ giác MNCB có MN//BC(cmt)
nên MNCB là hình thang có hai đáy là MN và BC(Định nghĩa hình thang)

\(\Leftrightarrow2x+4⋮2x-1\)
\(\Leftrightarrow2x-1+5⋮2x-1\)
\(\Leftrightarrow2x-1\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{1;0;3;-2\right\}\)
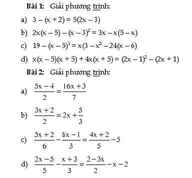
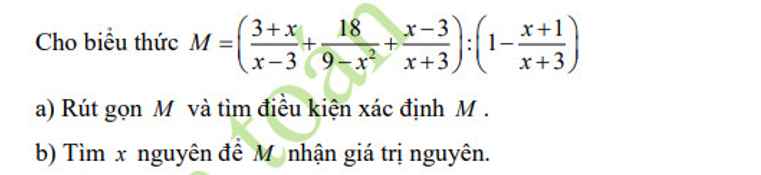



a/
\(\Leftrightarrow3-x-2-\left(10x-15\right)=0\)
\(\Leftrightarrow3-x-2-10x+15=0\)
\(16-11x=0\)
\(\Leftrightarrow x=\dfrac{16}{11}\)
d: \(\Leftrightarrow2x^2-10x-x^2+6x-9-3x+5x-x^2=0\)
=>-2x-9=0
=>-2x=9
hay x=-9/2
c: \(\Leftrightarrow19-x^3+15x^2-75x+125=x\left(3-x^2-24x+144\right)\)
\(\Leftrightarrow-x^3+15x^2-75x+144-3x+x^3+24x^2-144x=0\)
\(\Leftrightarrow39x^2-222x+144=0\)
\(\Delta=\left(-222\right)^2-4\cdot39\cdot144=26820>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{222-6\sqrt{745}}{78}=\dfrac{37-\sqrt{745}}{13}\\x_2=\dfrac{37+\sqrt{145}}{13}\end{matrix}\right.\)