Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ĐKXĐ:\(\left\{{}\begin{matrix}x+4\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-4\\x\ne1\end{matrix}\right.\)
b, ĐKXĐ:\(\left\{{}\begin{matrix}5\left(x-2\right)\ne0\\3\left(x+2\right)\ne0\\x^2-4\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\\x\ne\pm2\end{matrix}\right.\Leftrightarrow x\ne\pm2\)
c, ĐKXĐ:\(\left\{{}\begin{matrix}4x^2-8x+7\ne0\\4x^2-10x+7\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4\left(x^2-2x+\dfrac{7}{4}\right)\ne0\\4\left(x^2-\dfrac{10}{4}x+\dfrac{7}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2-2x+1\right)+\dfrac{3}{4}\ne0\\\left(x^2-2.\dfrac{10}{8}.x+\dfrac{25}{16}\right)+\dfrac{3}{16}\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+\dfrac{3}{4}\ne0\left(luôn.đúng\right)\\\left(x-\dfrac{5}{4}\right)^2+\dfrac{3}{16}\ne0\left(luôn.đúng\right)\end{matrix}\right.\)
\(\Leftrightarrow x\in R\)
a, đkxđ \(\left\{{}\begin{matrix}x+4\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-4\\x\ne1\end{matrix}\right.\)
b, đkxđ \(\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
c, đkxđ \(\left\{{}\begin{matrix}4x^2-8x+7\ne0\\4x^2-10x+7\ne0\end{matrix}\right.\)*luôn đúng *
Vậy \(x\in R\)

Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3

\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)

Phương trình chứa ẩn ở mẫu thì phải có ĐKXĐ để mẫu khác 0, và phải khử mẫu và còn phải loại những giá trị không thỏa mãn ĐK
Phương trình không chứa ẩn ở mẫu thì chỉ cần giải phương trình như bình thường




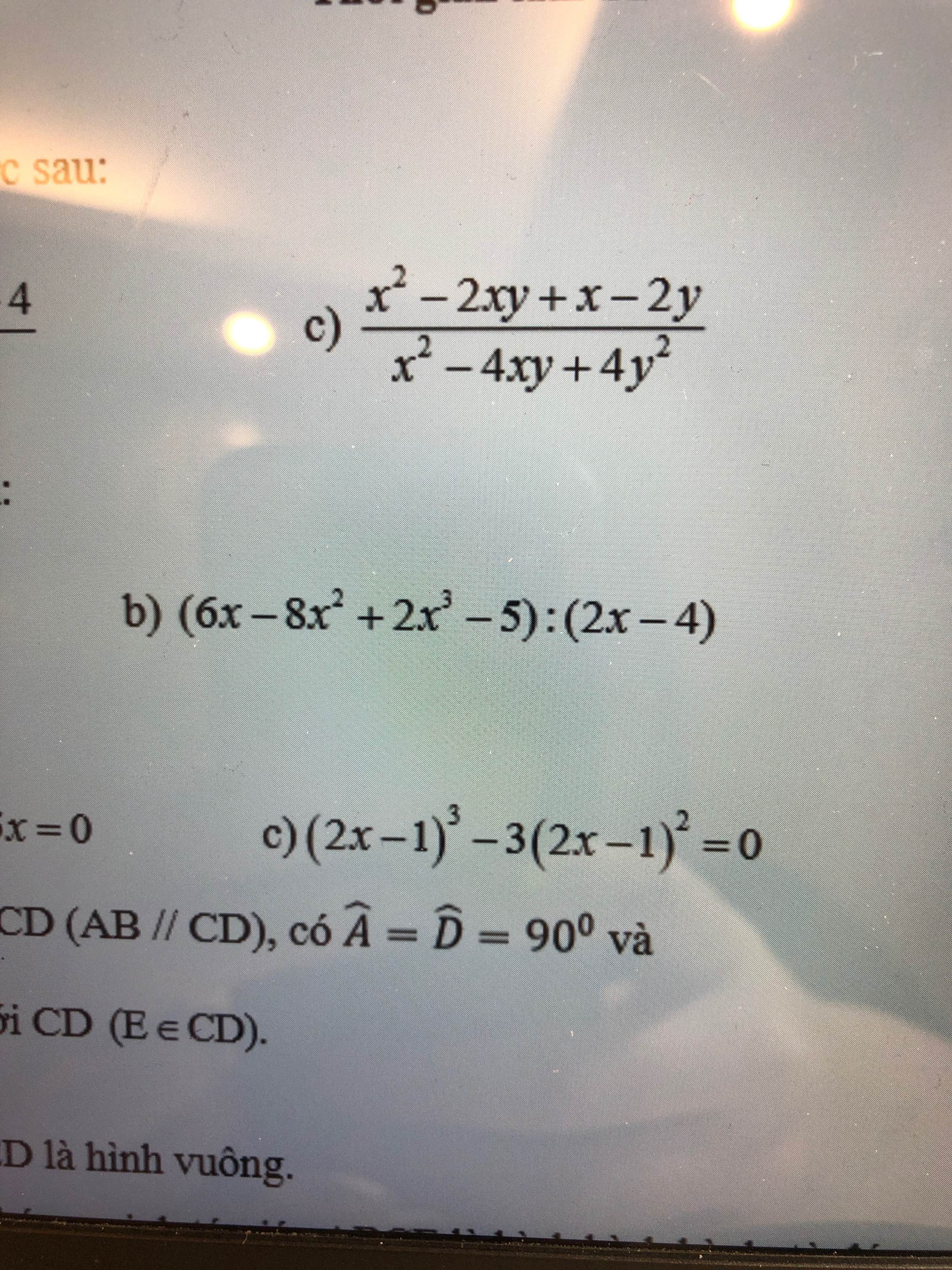

bạn đăng tách ra nhé
Bài 3 :
Ta có :\(1+\dfrac{1}{2+x}=\dfrac{12}{x^3+8}\)
đk : x khác -2
\(\Rightarrow x^3+8+x^2-2x+4=12\Leftrightarrow x^3+x^2-2x=0\)
\(\Leftrightarrow x\left(x^2+x-2\right)=0\Leftrightarrow x\left(x-1\right)\left(x+2\right)=0\Leftrightarrow x=0;x=1;x=-2\left(ktm\right)\)
Bài 2:
a,ĐKXĐ:\(\left\{{}\begin{matrix}x\ne0\\x\ne2\end{matrix}\right.\)
\(\dfrac{1}{x}+\dfrac{2}{x-2}=0\\ \Leftrightarrow\dfrac{x-2}{x\left(x-2\right)}+\dfrac{2x}{x\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{x-2+2x}{x\left(x-2\right)}=0\\ \Rightarrow3x-2=0\\ \Leftrightarrow x=\dfrac{2}{3}\left(tm\right)\)
b, ĐKXĐ:\(x\ne\pm2\)
\(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{5x-2}{4-x^2}\\ \Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2-5x}{x^2-4}\\ \Leftrightarrow\dfrac{x^2-3x+2-x^2-2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2-5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow\dfrac{-5x+2-2+5x}{\left(x-2\right)\left(x+2\right)}=0\\ \Leftrightarrow0=0\left(tm\right)\)