
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=180^0\)
Do đó: MAOB là tứ giác nội tiếp

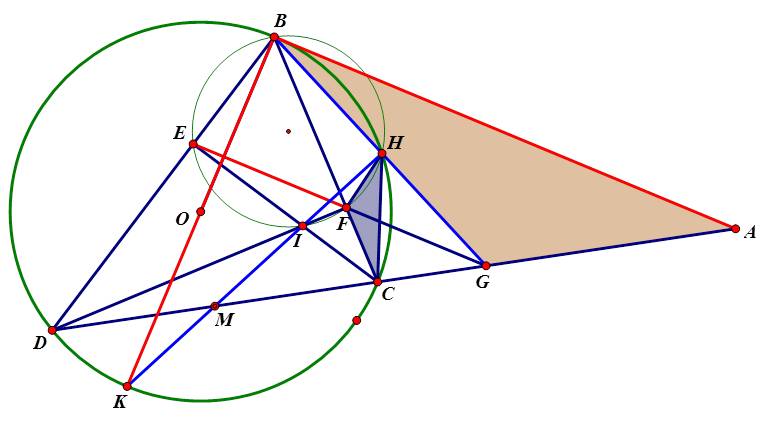
Từ điểm A nằm ngoài đường tròn (O; R) với OA > 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC < AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD.
a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.
b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GAB
c) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với CD

Xét tứ giác SAMO có
\(\widehat{OMS}=\widehat{OAS}=90^0\)
nên SAMO là tứ giác nội tiếp
hay S,A,M,O cùng thuộc 1 đường tròn
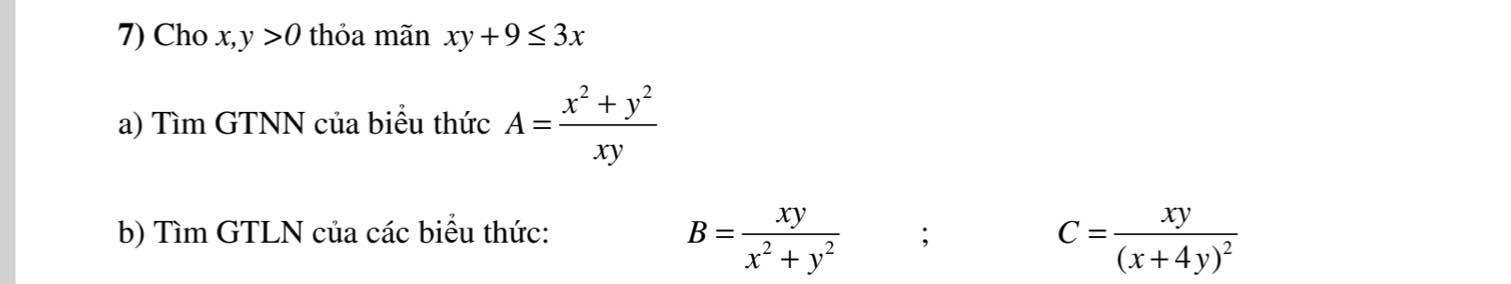 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺

 giúp mình ý a là đc ạ mình cảm ơn ạ
giúp mình ý a là đc ạ mình cảm ơn ạ
a) \(\text{∆}=\left(2m-1\right)^2-4\left(-m\right)\)
\(=4m^2+1>0\forall m\)
b) Vì phương trình có 2 nghiệm x1, x2 áp dụng hệ thức Vi-ét
\(\left\{{}\begin{matrix}x_1+x_2=-2m+1\\x_1x_2=-m\end{matrix}\right.\)
Ta có:
\(A=x^2_1+x^2_2-6x_1x_2\)
\(=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(-2m+1\right)^2-8.\left(-m\right)\)
\(=4m^2-4m+1+8m\)
\(=\left(2m+1\right)^2\ge0\forall m\)
Min \(A=0\Leftrightarrow m=-\dfrac{1}{2}\)