K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
2
MH
27 tháng 4 2022
a) \(\text{∆}=\left(2m-1\right)^2-4\left(-m\right)\)
\(=4m^2+1>0\forall m\)
b) Vì phương trình có 2 nghiệm x1, x2 áp dụng hệ thức Vi-ét
\(\left\{{}\begin{matrix}x_1+x_2=-2m+1\\x_1x_2=-m\end{matrix}\right.\)
Ta có:
\(A=x^2_1+x^2_2-6x_1x_2\)
\(=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(-2m+1\right)^2-8.\left(-m\right)\)
\(=4m^2-4m+1+8m\)
\(=\left(2m+1\right)^2\ge0\forall m\)
Min \(A=0\Leftrightarrow m=-\dfrac{1}{2}\)
29 tháng 4 2022
1.\(x=4-2\sqrt{3}-\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2=\left(\sqrt{3}-1\right)^2\)
\(A=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(2\sqrt{x}+1\right)}{\sqrt{x}-2}=2\sqrt{x}+1=2\sqrt{\left(\sqrt{3}-1\right)^2}+1=2\left(\sqrt{3}-1\right)+1=2\sqrt{3}-2+1=2\sqrt{3}-1\)
2.\(B=\dfrac{\sqrt{x^3}-\sqrt{x}+2x-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}^2\left(\sqrt{x}+2\right)-\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+2\right)\left(x-1\right)}{\sqrt{x}+2}=x-1\)
\(B=A+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+1+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+2\)
\(\Leftrightarrow x-2x\sqrt{x}-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-1\left(vô.lý\right)\end{matrix}\right.\) \(\rightarrow x=\sqrt{3}\)
M
1 tháng 5 2023
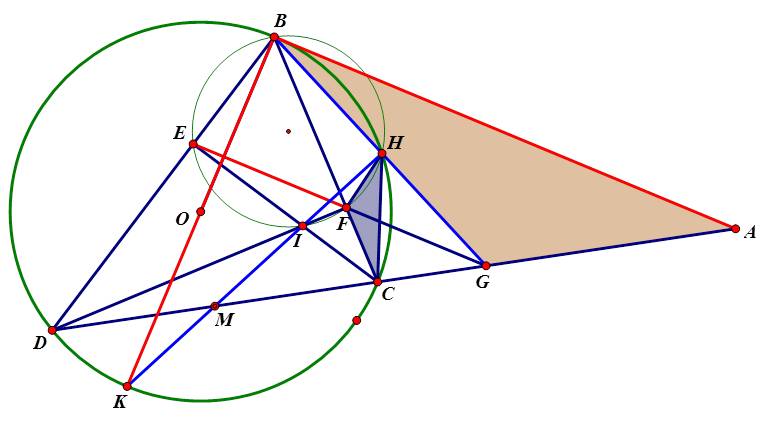
Từ điểm A nằm ngoài đường tròn (O; R) với OA > 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC < AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD.
a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.
b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GAB
c) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với CD
AH
Akai Haruma
Giáo viên
27 tháng 8 2021
Lời giải:
a. Để hàm trên là hàm bậc nhất thì $\frac{m-2}{m+3}\neq 0$
\(\Leftrightarrow \left\{\begin{matrix} m-2\neq 0\\ m+3\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 2\\ m\neq -3\end{matrix}\right.\)
b. Để hàm trên đồng biến thì $\frac{m-2}{m+3}>0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3>0\end{matrix}\right.\\ \left\{\begin{matrix} m-2<0\\ m+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m>2\\ m< -3\end{matrix}\right.\)
Để hàm trên nghịch biến thì $\frac{m-2}{m+3}< 0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3< 0\end{matrix}\right.\\ \left\{\begin{matrix} m-2< 0\\ m+3>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} -3> m>2(\text{vô lý}\\ -3< m< 2\end{matrix}\right.\Leftrightarrow -3< m< 2\)
15 tháng 5 2023
Thay x=7+căn 2022 vào pt, ta được:
\(49+14\sqrt{2022}+2022-7-\sqrt{2022}+3m-2=0\)
=>\(3m+2062+13\sqrt{2022}=0\)
=.\(m=\dfrac{-2062-13\sqrt{2022}}{3}\)
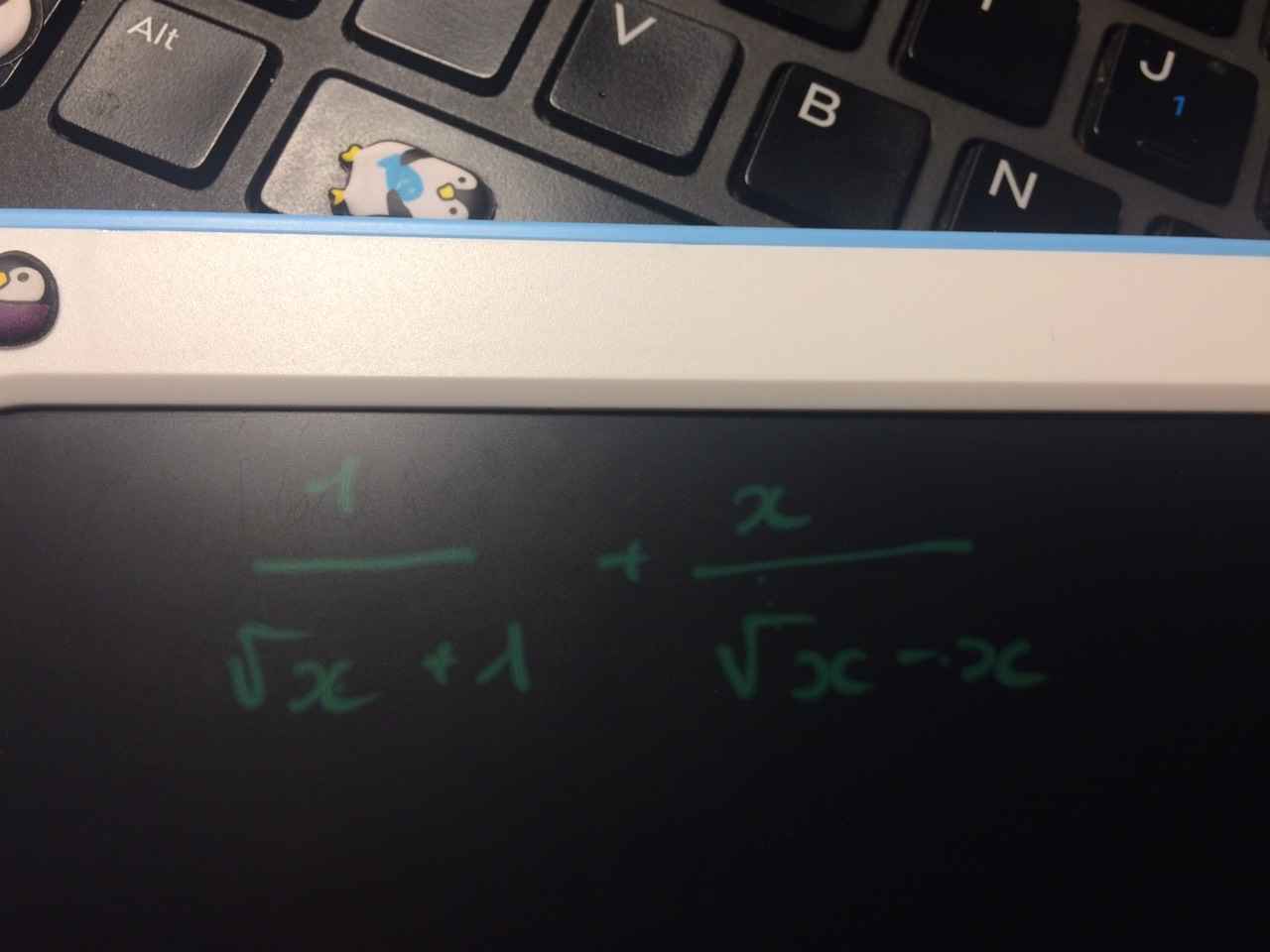
\(=\dfrac{1}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-x-\sqrt{x}}{x-1}=\dfrac{-x-1}{x-1}\)
\(\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{1-\sqrt{x}}\)
\(=\dfrac{1}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}-1-x-\sqrt{x}}{x-1}=\dfrac{-1-x}{x-1}\)