
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(\sqrt{\left(2+\sqrt{7}\right)^2}=2+\sqrt{7}=2\dfrac{\sqrt{7}}{1}\)
c. \(5\sqrt{x^2-6x+9}=5\sqrt{\left(x-3\right)^2}=5\left(x-3\right)=5x-15\)
d. \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-7\right)^2}=2-\sqrt{5}+\sqrt{5}-7=-5\)
a) \(\sqrt{\left(2+\sqrt{7}\right)^2}=\left|2+\sqrt{7}\right|=2+\sqrt{7}\)
b) \(\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
c) \(5\sqrt{x^2-6x+9}=5\sqrt{\left(x-3\right)^2}=5\left|x-3\right|=5\left(3-x\right)=15-5x\)(do x<3)
d) \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-7\right)^2}=2-\sqrt{5}+\sqrt{5}-7=-5\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-2\end{matrix}\right.\)
\(A=3-x_1^2-x_2^2\\ =3-\left(x_1^2+x_2^2\right)\\ =3-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =3-\left[\left(-\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =3-\left(\dfrac{1}{4}+4\right)\\ =3-\dfrac{17}{4}\\ =-\dfrac{5}{4}\)
\(B=\left(x_1-x_2\right)^2\\ =x_1^2+x_2^2-2x_1x_2\\ =\left(x_1+x_2\right)^2-4x_1x_2\\ =\left(\dfrac{1}{2}\right)^2-4.\left(-2\right)\\ =\dfrac{1}{4}+8\\ =\dfrac{33}{4}\)
\(D=\left(1+x_1\right)\left(2-x_1\right)+\left(1+x_2\right)\left(2-x_2\right)\\ =2+x_1-x_1^2+2+x_2-x_2^2\\ =4+\left(x_1+x_2\right)-\left(x_1^2+x_2^2\right)\\ =4+\dfrac{1}{2}-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\dfrac{9}{2}-\left[\left(\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =\dfrac{9}{2}-\dfrac{17}{4}\\ =\dfrac{1}{4}\)

1: \(A=\dfrac{\left(x+1\right)^3}{\left(x+1\right)^2}=x+1\)
\(B=\dfrac{\left(x+1\right)\cdot\left(x^2-x+1\right)}{x+1}=x^2-x+1\)
2: A=B
=>x^2-x+1=x+1
=>x^2-2x=0
=>x=0 hoặc x=2

Hình vẽ nhỏ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.
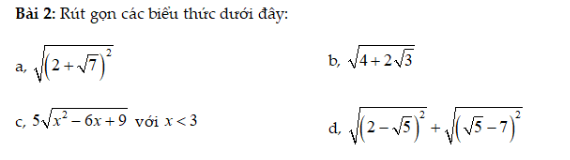

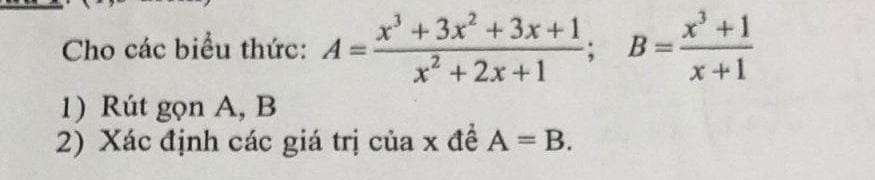

 X
X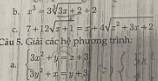
=> MO là tia p/giác của góc AMB,OM là tia p/giác của góc AOB =>AMO=BMO=AMB/2=40/2=20
Vì AM là tiếp tuyến của đ.tròn (O)tại A =>tam giác AOM vuông tại A =>AMO+AOM=90=>AOM=90-20=70
Vậy góc AMO=20,góc AOM=70
b) Ta có OM là tia p/giác của góc AOB( câu a)=>AOB=2AOM=2x70=140
Vì AOB là góc ở tâm chắn cung AmB nên sđAmB=AOB=140
=>sđAnB=360-140=220