
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
\(\left[\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1}\right]:\dfrac{2\sqrt{3x}}{x-1}\)
\(=\left(\dfrac{x+\sqrt{x}+x-\sqrt{x}}{x-1}\right).\dfrac{x-1}{2\sqrt{3x}}\)
\(=\dfrac{2x}{x-1}.\dfrac{x-1}{2\sqrt{3x}}=\dfrac{\sqrt{x}}{\sqrt{3}}=\dfrac{\sqrt{3x}}{3}\)


\(\frac{\left(5\sqrt{7}+7\sqrt{5}\right)}{\sqrt{35}}\)
= \(\frac{\sqrt{5}.\left(\sqrt{35}+7\right)}{\sqrt{35}}\)
= \(\frac{\sqrt{35}+7}{\sqrt{7}}\)
= \(\sqrt{5}+\sqrt{7}\)
\(\frac{5\sqrt{7}+7\sqrt{5}}{\sqrt{35}}=\frac{\sqrt{5}.\sqrt{5}.\sqrt{7}+\sqrt{7}.\sqrt{7}.\sqrt{5}}{\sqrt{35}}.\)
\(=\frac{\sqrt{5}.\sqrt{35}+\sqrt{7}.\sqrt{35}}{\sqrt{35}}\)
\(=\frac{\sqrt{35}\left(\sqrt{5}+\sqrt{7}\right)}{\sqrt{35}}=\sqrt{5}+\sqrt{7}\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-2\end{matrix}\right.\)
\(A=3-x_1^2-x_2^2\\ =3-\left(x_1^2+x_2^2\right)\\ =3-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =3-\left[\left(-\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =3-\left(\dfrac{1}{4}+4\right)\\ =3-\dfrac{17}{4}\\ =-\dfrac{5}{4}\)
\(B=\left(x_1-x_2\right)^2\\ =x_1^2+x_2^2-2x_1x_2\\ =\left(x_1+x_2\right)^2-4x_1x_2\\ =\left(\dfrac{1}{2}\right)^2-4.\left(-2\right)\\ =\dfrac{1}{4}+8\\ =\dfrac{33}{4}\)
\(D=\left(1+x_1\right)\left(2-x_1\right)+\left(1+x_2\right)\left(2-x_2\right)\\ =2+x_1-x_1^2+2+x_2-x_2^2\\ =4+\left(x_1+x_2\right)-\left(x_1^2+x_2^2\right)\\ =4+\dfrac{1}{2}-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\dfrac{9}{2}-\left[\left(\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =\dfrac{9}{2}-\dfrac{17}{4}\\ =\dfrac{1}{4}\)

\(a,2x^2+3x-9=0\\ \Leftrightarrow\left(2x^2+6x\right)-\left(3x+9\right)=0\\ \Leftrightarrow2x\left(x+3\right)-3\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(b,6x-12x^2=0\\ \Leftrightarrow6x\left(1-2x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(c,8x^2-1=0\\ \Leftrightarrow x^2=\dfrac{1}{8}\\ \Leftrightarrow x=\pm\dfrac{\sqrt{2}}{4}\)
\(d,x^4-7x^2-18=0\\ \Leftrightarrow\left(x^4-3x^3\right)+\left(3x^3-9x^2\right)+\left(2x^2-6x\right)+\left(6x-18\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^3+3x^2+2x+6\right)=0\\ \Leftrightarrow\left(x-3\right)\left[x^2\left(x+3\right)+2\left(x+3\right)\right]=0\\ \Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x^2+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x^2=-2\left(vô.lí\right)\end{matrix}\right.\)

a: \(\Leftrightarrow2x^2+6x-3x-9=0\)
=>(x+3)(2x-3)=0
=>x=3/2 hoặc x=-3
b: \(\Leftrightarrow6x\left(1-2x\right)=0\)
=>x=0 hoặc 1-2x=0
=>x=0 hoặc x=1/2
c: \(\Leftrightarrow8x^2=1\)
\(\Leftrightarrow x^2=\dfrac{2}{16}\)
hay \(x\in\left\{\dfrac{\sqrt{2}}{4};-\dfrac{\sqrt{2}}{4}\right\}\)
d: \(\Leftrightarrow x^4-9x^2+2x^2-18=0\)
\(\Leftrightarrow x^2-9=0\)
=>x=3 hoặc x=-3


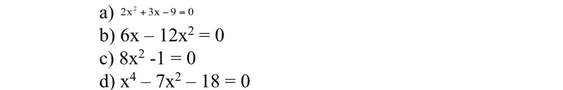

to quá bn ạ