
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+x}-2}{4x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{4+x}-2\right)\left(\sqrt{4+x}+2\right)}{4x\left(\sqrt{4+x}+2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{x}{4x\left(\sqrt{4+x}+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{1}{4\left(\sqrt{4+x}+2\right)}=\dfrac{1}{4\left(\sqrt{4+0}+2\right)}=\dfrac{1}{16}\)
b.
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x+7}-2\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}\)
\(=\dfrac{1}{\sqrt[3]{8^2}+2\sqrt[3]{8}+4}=\dfrac{1}{12}\)



a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ


Trên thực tế điểm P nằm ở đâu trên SC đều không quan trọng
Ta có: \(\overrightarrow{AI}=\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\dfrac{AI}{AB}=\dfrac{1}{3}\)
\(\overrightarrow{DJ}=\dfrac{2}{3}\overrightarrow{DA}\Rightarrow\overrightarrow{AJ}=\dfrac{1}{3}\overrightarrow{AD}\Rightarrow\dfrac{AJ}{AD}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{AI}{AB}=\dfrac{AJ}{AD}\Rightarrow IJ||BD\) (Talet đảo) (1)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AP\) (2)
(1);(2) \(\Rightarrow IJ\perp AP\) hay góc giữa 2 đường thẳng bằng \(\dfrac{\pi}{2}\)


\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)


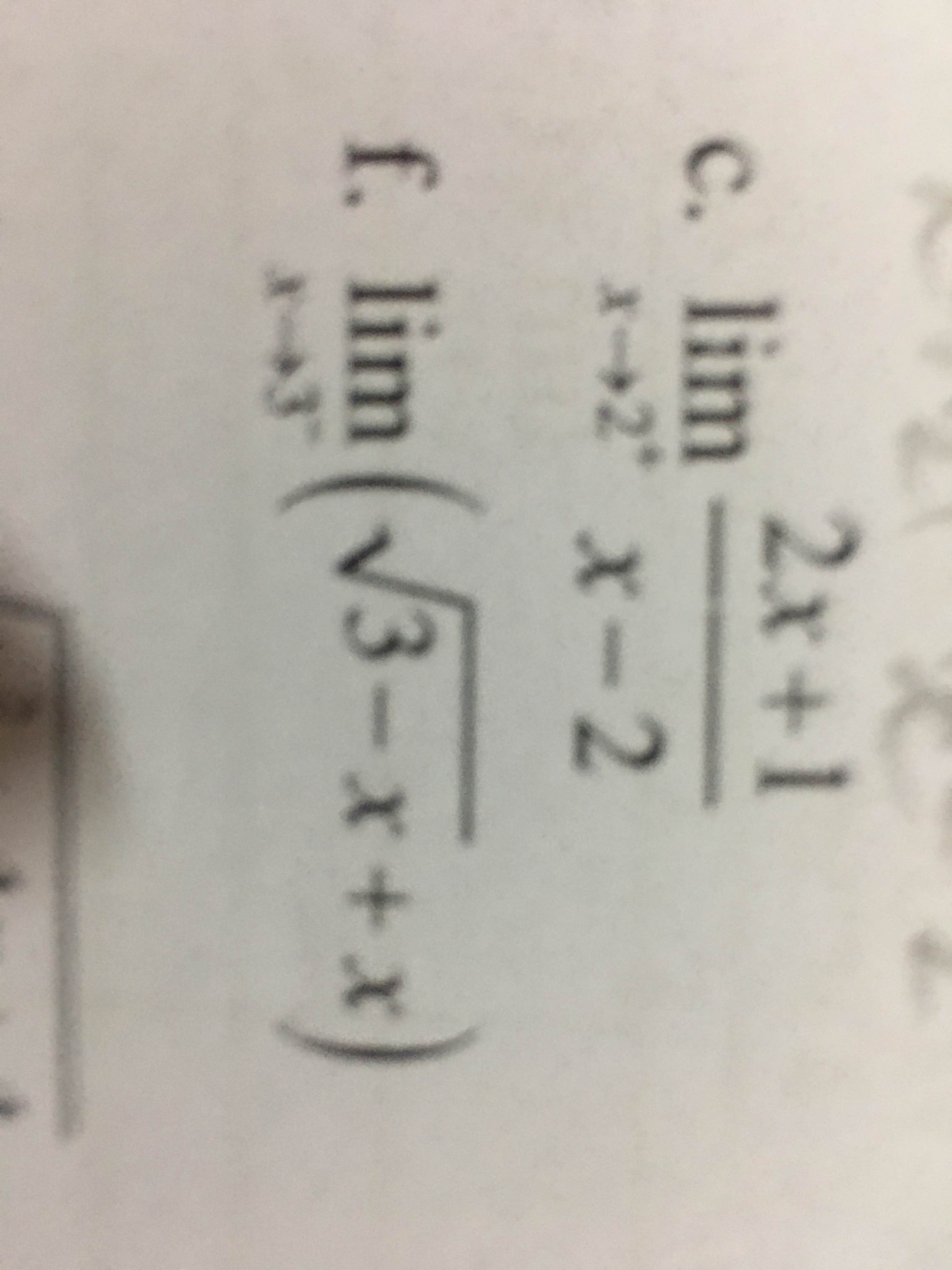





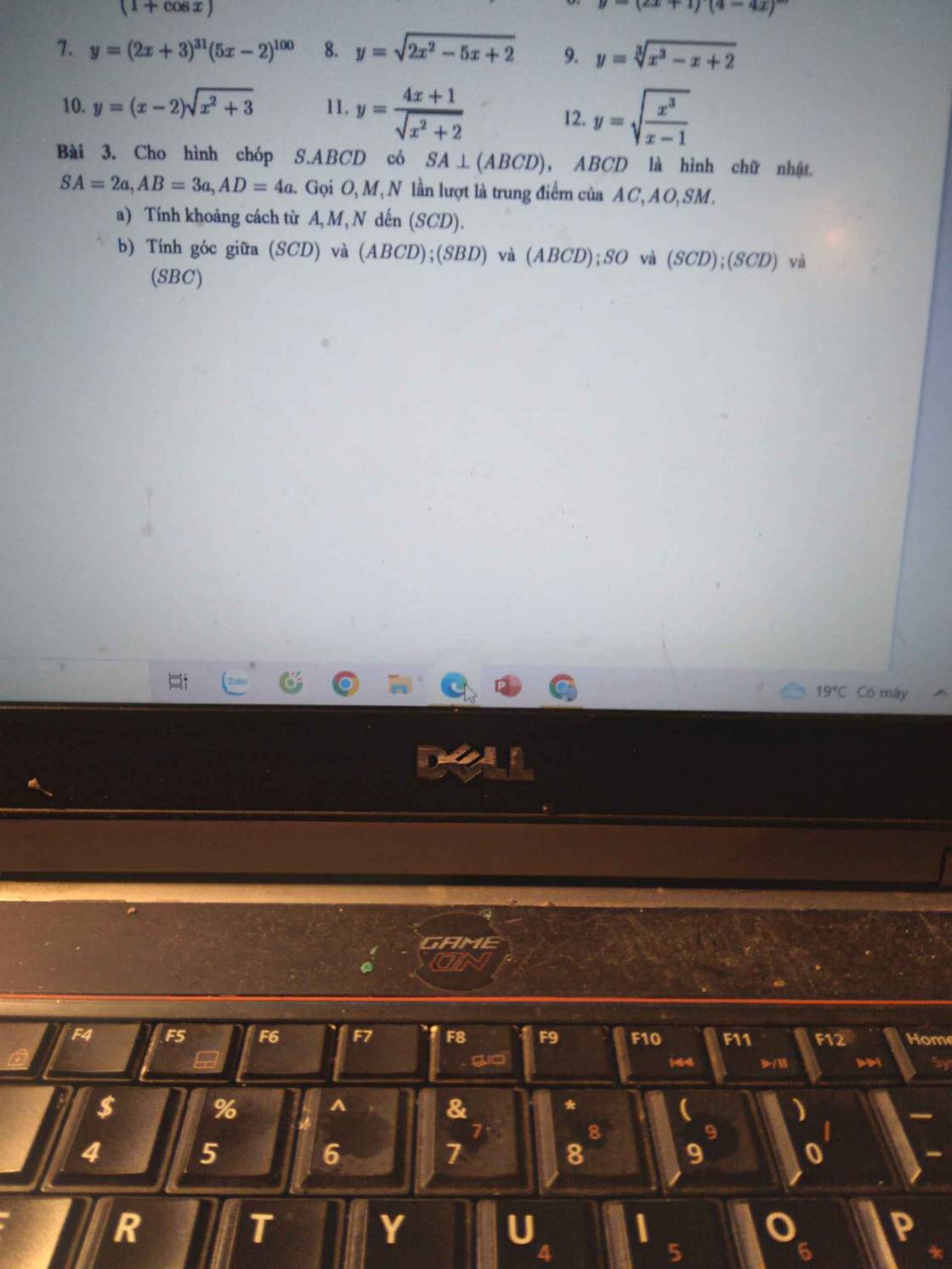 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ



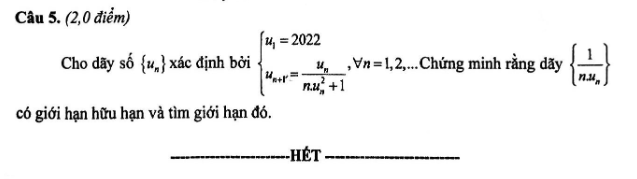 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ
\(\dfrac{n}{2n-1}>\dfrac{n}{2n}=\dfrac{1}{2}\)
\(\Rightarrow x_{n+1}>\dfrac{1}{2}.\left(\dfrac{x_n^2+2}{x_n}\right)\ge\dfrac{1}{2}.\dfrac{2\sqrt{2x_n^2}}{x_n}=\sqrt{2}\)
Dãy bị chặn dưới bởi \(\sqrt{2}\)
Ta sẽ chứng minh dãy đã cho là dãy giảm, hay \(x_{n+1}-x_n< 0\) với \(n>1\)
\(\Leftrightarrow\dfrac{n}{2n-1}\left(\dfrac{x_n^2+2}{x_n}\right)-x_n< 0\Leftrightarrow\left(1-n\right)x_n^2+2n< 0\)
\(\Leftrightarrow x_n^2>\dfrac{2n}{n-1}\Leftrightarrow x_n>\sqrt{\dfrac{2n}{n-1}}\)
Do \(x_n=\dfrac{n-1}{2\left(n-1\right)-1}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)=\dfrac{n-1}{2n-3}.\left(\dfrac{x_{n-1}^2+2}{x_{n-1}}\right)\ge\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}\)
Nên ta chỉ cần chứng minh: \(\dfrac{2\sqrt{2}\left(n-1\right)}{2n-3}>\sqrt{\dfrac{2n}{n-1}}\)
\(\Leftrightarrow6n-8>0\) (đúng)
Vậy dãy đã cho là dãy giảm
Dãy giảm và bị chặn dưới nên có giới hạn
Gọi giới hạn của dãy là L, lấy giới hạn 2 vế biểu thức truy hồi:
\(\lim\left(x_{n+1}\right)=\lim\left(\dfrac{n}{2n-1}.\dfrac{x_n^2+2}{x_n}\right)\Rightarrow L=\dfrac{1}{2}\left(\dfrac{L^2+2}{L}\right)\)
\(\Rightarrow L^2=2\Rightarrow L=\sqrt{2}\)
em cảm ơn thầyyy