K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 9 2021
\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\left(1-\dfrac{1}{\sqrt{x}}\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{4}{\sqrt{x}+1}\)
20 tháng 9 2021
\(a,A=\left(1;2\right)\Leftrightarrow x=1;y=2\\ \Leftrightarrow2=\left(m+1\right)-2m+3\\ \Leftrightarrow-m+4=2\Leftrightarrow m=2\)
\(c,\)Giả sử điểm cố định là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m+1\right)x_0-2m+3\\ \Leftrightarrow y_0=mx_0+x_0-2m+3\\ \Leftrightarrow m\left(x_0-2\right)+\left(x_0-y_0+3\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0-y_0+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=5\end{matrix}\right.\Leftrightarrow B\left(2;5\right)\)
Vậy \(\left(d\right)\) luôn đi qua điểm \(B\left(2;5\right)\) cố định
\(d,\) Pt hoành độ giao điểm:
\(2=\left(2+1\right)x-2\cdot2+3\\ \Leftrightarrow2=3x-1\Leftrightarrow x=1\\ \Leftrightarrow C\left(1;2\right)\)
Vậy ...
TN
1
MH
27 tháng 4 2022
Ta có:
\(x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=4\)
\(\left(x^2-2+\dfrac{1}{x^2}\right)+\left(y^2-2+\dfrac{1}{y^2}\right)+4=4\)
\(\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)\ge0\forall y\end{matrix}\right.\)
Dấu "="⇔ \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\end{matrix}\right.\)
\(\Leftrightarrow x^2=y^2=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\x=y=-1\\x=1,y=-1\\x=-1,y=1\end{matrix}\right.\)
Thay vào phương trình 1
⇒ \(x=y=1\)
1 tháng 7 2023
a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC
=>AB^2/AC^2=BH/CH
b: ΔAHB vuông tại H có HD là đường cao
nên BH^2=BD*BA
=>BD=BH^2/BA
ΔAHC vuông tại H có HE là đường cao
nên CH^2=CE*CA
=>CE=CH^2/CA
BD/CE=BH^2/BA:CH^2/CA
\(=\dfrac{BH^2}{BA}\cdot\dfrac{CA}{CH^2}=\left(\dfrac{BA}{CA}\right)^4\cdot\dfrac{CA}{BA}=\left(\dfrac{BA}{CA}\right)^3\)
NV
15 tháng 3 2023
Đổi 1 giờ 30 phút=90 phút
- Số phần bể Giang làm đầy trong 1 phút: \(\dfrac{1}{30}\) bể.
- Số phần bể Sơn làm đầy trong 1 phút: \(\dfrac{1}{45}\) bể.
- Số phần bể Tài làm đầy trong 1 phút: \(\dfrac{1}{90}\) bể.
- Thời gian làm đầy bể khi cả 3 người cùng làm việc:
\(1:\left(\dfrac{1}{30}+\dfrac{1}{45}+\dfrac{1}{90}\right)=15\left(phút\right)\)
Chọn A.
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
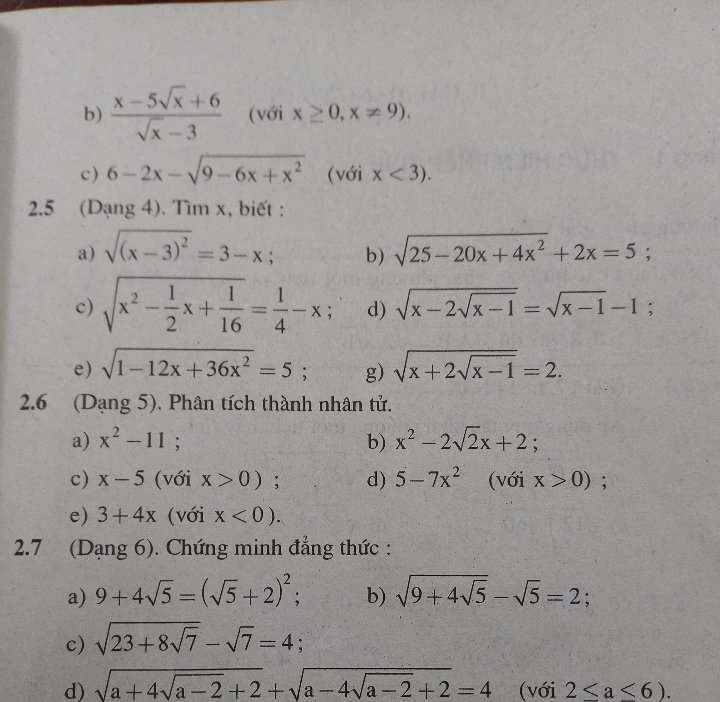
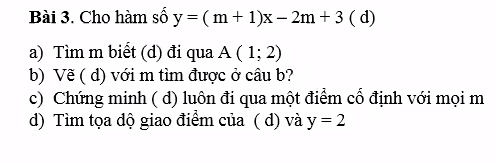
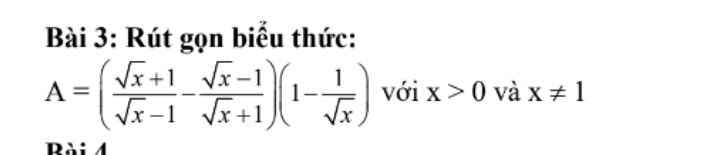
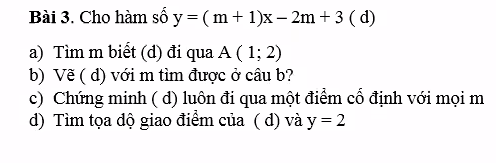
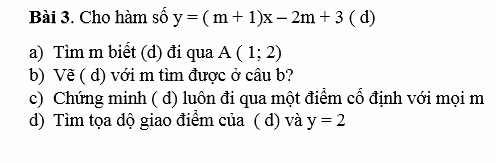
2.7
a/ $9+4\sqrt{5}=2^2+2.2\sqrt{5}+(\sqrt{5})^2=(2+\sqrt{5})^2$
b/ $\sqrt{9+4\sqrt{5}}-\sqrt{5}=\sqrt{(2+\sqrt{5})^2}-\sqrt{5}$
$=|2+\sqrt{5}|-\sqrt{5}=2+\sqrt{5}-\sqrt{5}=2$
c/ $\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{4^2+2.4\sqrt{7}+(\sqrt{7})^2}-\sqrt{7}=\sqrt{(4+\sqrt{7})^2}-\sqrt{7}$
$=4+\sqrt{7}-\sqrt{7}=4$
d.
$\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}$
$=\sqrt{(a-2)+2.2\sqrt{a-2}+2^2}+\sqrt{(a-2)-2.2\sqrt{a-2}+2^2}$
$=\sqrt{(\sqrt{a-2}+2)^2}+\sqrt{(\sqrt{a-2}-2)^2}$
$=|\sqrt{a-2}+2|+|\sqrt{a-2}-2|$
$=\sqrt{a-2}+2+2-\sqrt{a-2}=4$ (do $a\leq 6$ nên $\sqrt{a-2}-2\leq 0$ nên $|\sqrt{a-2}-2|=2-\sqrt{a-2}$)
2.5
a.
$\sqrt{(x-3)^2}=3-x$
$\Leftrightarrow |x-3|=3-x$
$\Leftrightarrow 3-x\geq 0$
$\Leftrightarrow x\leq 3$
b.
$\sqrt{25-20x+4x^2}+2x=5$
$\Leftrightarrow \sqrt{(2x-5)^2}=5-2x$
$\Leftrightarrow |2x-5|=5-2x$
$\Leftrightarrow 5-2x\geq 0$
$\Leftrightarrow x\leq \frac{2}{5}$
c.
$\sqrt{x^2-\frac{1}{2}x+\frac{1}{16}}=\frac{1}{4}-x$
$\Leftrightarrow \sqrt{(x-\frac{1}{4})^2}=\frac{1}{4}-x$
$\Leftrightarrow |x-\frac{1}{4}|=\frac{1}{4}-x$
$\Leftrightarrow \frac{1}{4}-x\geq 0$
$\Leftrightarrow x\leq \frac{1}{4}$