K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Bài 1:
\((n+1)^n-1=n[(n+1)^{n-1}+(n+1)^{n-2}+....+(n+1)+1]\)
Giờ ta chỉ cần cmr \((n+1)^{n-1}+(n+1)^{n-2}+...+(n+1)+1\vdots n\)
Thật vậy:
\((n+1)^{n-1}+(n+2)^{n-2}+...+(n+1)+1\equiv 1^{n-1}+1^{n-2}+...+1^1+1=n\equiv 0\pmod n\)
Do đó ta có đpcm.
AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Bài 2 em xem lại. Số $2^{n(2^n-1)}$ chỉ toàn ước có dạng $2^k$ với $k=0,1,..., n(2^n-1)$ trong khi đó $(2^n-1)^2$ là số lẻ.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
Phương trình hoành độ giao điểm d1 và d2:
\(-3x-7=2x+3\)
\(\Rightarrow-5x=10\Rightarrow x=-2\)
Thế vào \(y=-3x-7=-3.\left(-2\right)-7=-1\)
Vậy \(M\left(-2;-1\right)\)
1 tháng 10 2021
Thay x=1 vào y=2x-3, ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(m-3+4=-1\)
hay m=-2
25 tháng 5 2021
`A=1/(x+sqrtx)+(2sqrtx)/(x-1)-1/(x-sqrtx)`
`=(sqrtx-1+2x-sqrtx-1)/(sqrtx(x-1))`
`=(2x-2)/(sqrtx(x-1))`
`=2/sqrtx`
`b)A=1`
`<=>2/sqrtx=1`
`<=>sqrtx=2`
`<=>x=4(tm)`
6 tháng 7 2023
1.4:
a: CH=16^2/24=256/24=32/3
BC=24+32/3=104/3
AC=căn 32/3*104/3=16/3*căn 13
b: BC=12^2/6=24
AC=căn 24^2-12^2=12*căn 3
CH=24-6=18
29 tháng 10 2021
2: Để (d)//y=(m2+1)x-4 thì \(\left\{{}\begin{matrix}m^2=1\\m-5\ne-4\end{matrix}\right.\Leftrightarrow m=1\)
16 tháng 4 2023
=>5x^2-6x-11=0
=>5x^2-11x+5x-11=0
=>(5x-11)(x+1)=0
=>x=11/5 hoặc x=-1
13 tháng 11 2021
\(a,ĐK:x\ge2\\ PT\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}=\sqrt{3}\\ \Leftrightarrow\sqrt{x-2}=\sqrt{3}\\ \Leftrightarrow x-2=3\\ \Leftrightarrow x=5\left(tm\right)\\ b,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\sqrt{x-3}-\sqrt{x-3}=6\\ \Leftrightarrow3\sqrt{x-3}=6\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\\ c,ĐK:x\ge-4\\ PT\Leftrightarrow4\sqrt{x+4}+2\sqrt{x+4}-2\sqrt{x+4}=1\\ \Leftrightarrow4\sqrt{x+4}=1\\ \Leftrightarrow\sqrt{x+4}=\dfrac{1}{4}\Leftrightarrow x+1=\dfrac{1}{16}\Leftrightarrow x=-\dfrac{15}{16}\left(tm\right)\\ d,ĐK:x\ge0\\ PT\Leftrightarrow\sqrt{3x}+\sqrt{3x}-4\sqrt{3x}=-2\\ \Leftrightarrow-2\sqrt{3x}=-2\\ \Leftrightarrow\sqrt{3x}=1\Leftrightarrow3x=1\Leftrightarrow x=\dfrac{1}{3}\left(tm\right)\)
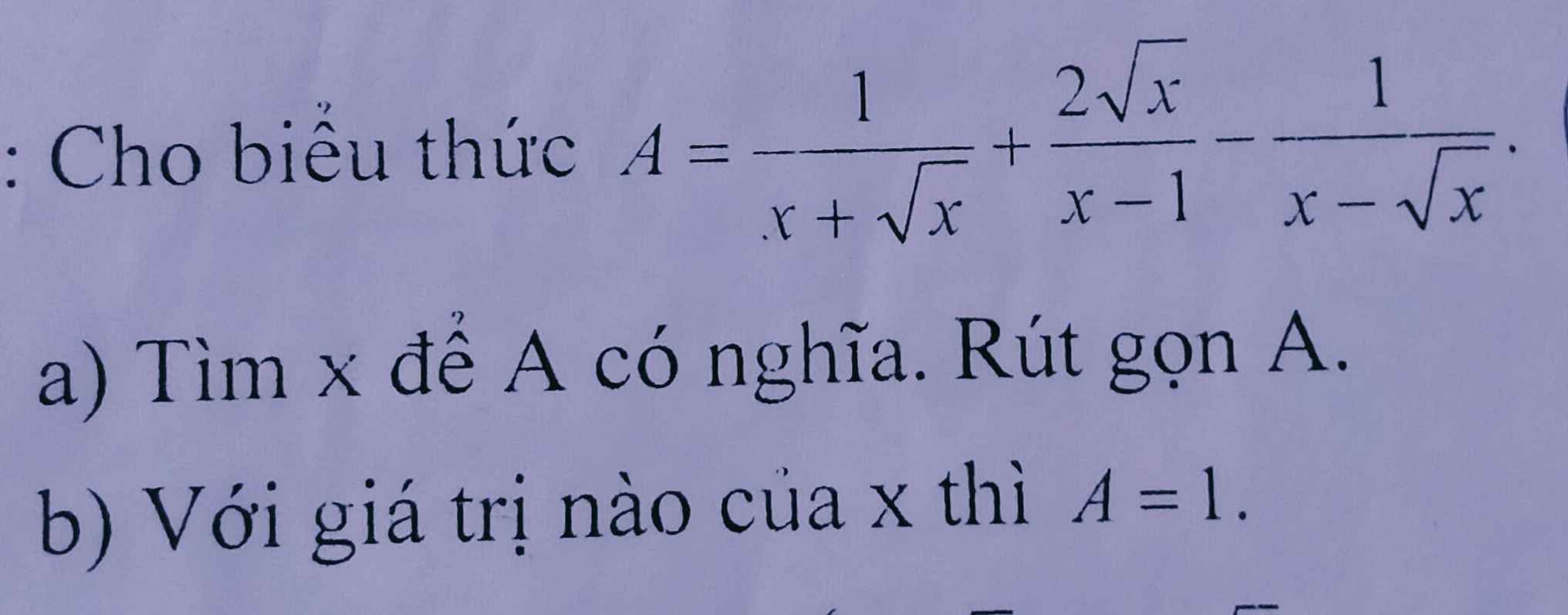
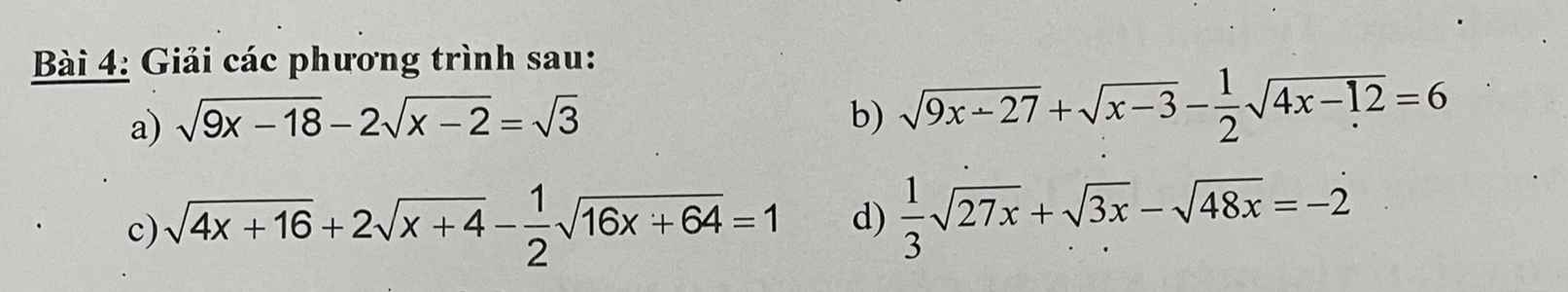
Áp dụng bất đẳng thức Cosi ta có :
\(x^4+1\ge2x^2;x^2+1\ge\left|x\right|\Rightarrow x^4+3\ge4\left|x\right|\)
Tương tự : \(y^4+3\ge4\left|y\right|\)
\(\Rightarrow x^4+y^4+6\ge4\left(\left|x\right|+\left|y\right|\right)\left(1\right)\)
Từ (1) suy ra \(x^4+y^4+6\ge4\left(x-y\right)\Rightarrow P\le\dfrac{1}{4}\)
Dấu = xảy ra \(x=1;y=-1\)
Từ (1) suy ra \(x^4+y^4+6\ge4\left(y-x\right)\Rightarrow P\ge-\dfrac{1}{4}\)
Dấu = xảy ra \(x=-1;y=1\)