K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 12 2021
\(a,m=0\Leftrightarrow y=3x+2\)
Vì \(3>0\) nên hàm đồng biến
\(b,\text{Thay }x=-1;y=3\\ \Leftrightarrow-m-3+2=3\Leftrightarrow m=-4\\ c,\text{PT giao Ox: }y=0\Leftrightarrow x=-\dfrac{2}{m+3}\Leftrightarrow A\left(-\dfrac{2}{m+3};0\right)\Leftrightarrow OA=\dfrac{2}{\left|m+3\right|}\\ \text{PT giao Oy: }x=0\Leftrightarrow y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\\ \text{Ta có }S_{OAB}=4\\ \Leftrightarrow\dfrac{1}{2}OA\cdot OB=4\Leftrightarrow\dfrac{2}{\left|m+3\right|}\cdot2=8\\ \Leftrightarrow\dfrac{4}{\left|m+3\right|}=8\\ \Leftrightarrow\left|m+3\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
DT
10 tháng 4 2023
Để phương trình có 2 nghiệm phân biệt thì:
\(\Delta>0\\ \Leftrightarrow\left(-5\right)^2-4.1.\left(m+4\right)>0\\ \Leftrightarrow25-4m-16>0\\\Leftrightarrow9-4m>0\\ \Leftrightarrow m< \dfrac{9}{4}\)
Theo viét:
\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m+4\end{matrix}\right.\)
c,
\(\left|x_1-x_2\right|=3\\ \Leftrightarrow\left(x_1-x_2\right)^2=9\\ \Leftrightarrow x_1^2-2x_1x_2+x_2^2=9\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\\ \Leftrightarrow5^2-4\left(m+4\right)=9\\ \Leftrightarrow25-4m-16=9\\ \Leftrightarrow m=0\left(nhận\right)\)
d.
\(\left|x_1\right|+\left|x_2\right|=4\\ \)
Xét trường hợp 1: hai nghiệm đều dương:
ta có:
\(x_1+x_2=4\)
5 = 4 (vô lý)
Loại trường hợp này.
Xét trường hợp 2: hai nghiệm đều âm, tương tự ta loại trường hợp này.
Xét trường hợp 3:
\(x_1< 0< x_2\)
=> \(x_2-x_1=4\)
<=> \(x_2+x_1-2x_1=4\)
=> \(5-2x_1=4\)
=> \(x_1=\dfrac{1}{2}\)
\(x_2< 0< x_1\)
\(x_1-x_2=4\\ \Leftrightarrow x_1+x_2-2x_2=4\\ \Leftrightarrow5-2x_2=4\\ \Rightarrow x_2=\dfrac{1}{2}\)
Có: \(x_1x_2=m+4\\\)
<=> \(\dfrac{1}{2}.\dfrac{1}{2}=m+4\)
=> m = -3,75 (nhận)
e.
Theo viét và theo đề ta có:
\(\left\{{}\begin{matrix}3x_1+4x_2=6\left(1\right)\\x_1+x_2=5\left(2\right)\\x_1x_2=m+4\left(3\right)\end{matrix}\right.\)
Từ (1) có \(x_1=\dfrac{6-4x_2}{3}=2-\dfrac{4}{3}x_2\) (x)
Thế (x) vào (2) được \(2-\dfrac{4}{3}x_2+x_2=5\)
=> \(x_2=-9\) (xx)
Thế (xx) vào (1) được \(3x_1+4.\left(-9\right)=6\)
=> \(x_1=14\) (xxx)
Thế (xx) và (xxx) vào (3) được:
\(14.\left(-9\right)=m+4\)
=> m = -130 (nhận)
h.
\(x_1\left(1-3x_2\right)+x_2\left(1-3x_1\right)=m^2-23\)
<=> \(x_1-3x_1x_2+x_2-3x_1x_2=m^2-23\)
<=> \(x_1+x_2-6x_1x_2=m^2-23\)
<=> \(5-6.\left(m+4\right)=m^2-23\)
<=> \(5-6m-20-m^2+23=0\)
<=> \(-m^2-6m+8=0\)
\(\Delta=\left(-6\right)^2-4.\left(-1\right).8=68\)
\(m_1=\dfrac{6+\sqrt{68}}{2.\left(-1\right)}=-3-\sqrt{17}\left(nhận\right)\)
\(m_2=\dfrac{6-\sqrt{68}}{2.\left(-1\right)}=-3+\sqrt{17}\left(nhận\right)\)
☕T.Lam
Mình không chắc chắn ở câu d, mình lên đây để ôn bài thi tiện thể giúp được bạn phần nào.
26 tháng 9 2021
c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=5\)
\(\Leftrightarrow\sqrt{x-4}+2=5\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
hay x=13
26 tháng 9 2021
c: Ta có: √x+4√x−4=5x+4x−4=5
⇔√x−4+2=5⇔x−4+2=5
⇔√x−4=3⇔x−4=3
⇔x−4=9⇔x−4=9
hay x=13
18 tháng 12 2022
b: Tọa độ giao là:
5x-4=2x+2 và y=2x+2
=>x=2 và y=6
c: Vì (d2)//d nên (d2): y=2x+b
Thay x=1 và y=3 vào (d2), ta được:
b+2=3
=>b=1
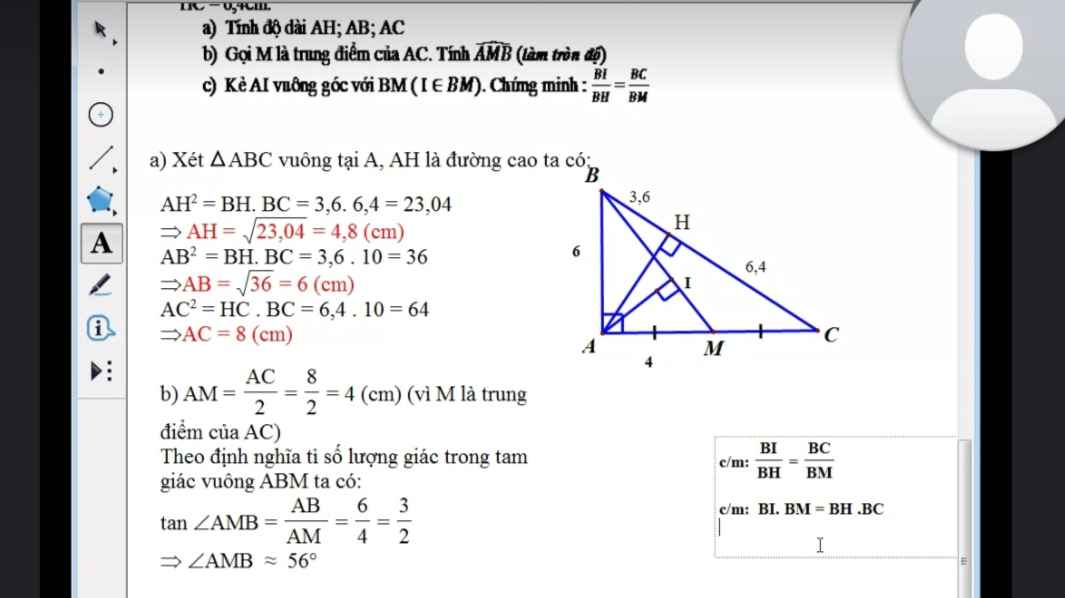
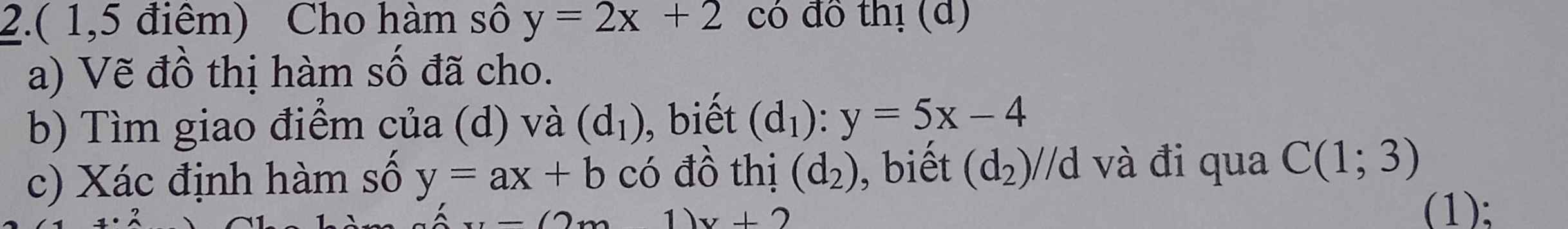
c, Áp dụng HTL ta được \(\left\{{}\begin{matrix}BI\cdot BM=AB^2\\BH\cdot BC=AB^2\end{matrix}\right.\Rightarrow BI\cdot BM=BH\cdot BC\)
\(\Rightarrow\dfrac{BI}{BH}=\dfrac{BC}{BM}\)
c: Xét ΔABM vuông tại A có AI là đường cao
nên \(BI\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BI\cdot BM=BH\cdot BC\)
hay \(\dfrac{BI}{BH}=\dfrac{BC}{BM}\)