K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
JP
1
JP
0
TN
2
27 tháng 10 2021
a: \(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{2\sqrt{x}+2+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}}{x-1}\)
27 tháng 10 2021
\(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{2\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt{3+2\sqrt{2}}}{3+2\sqrt{2}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}}{2+2\sqrt{2}}\)
\(\Rightarrow P=\dfrac{\sqrt{2}+1}{2\left(\sqrt{2}+1\right)}\)
\(\Rightarrow P=\dfrac{1}{2}\)
8 tháng 11 2021
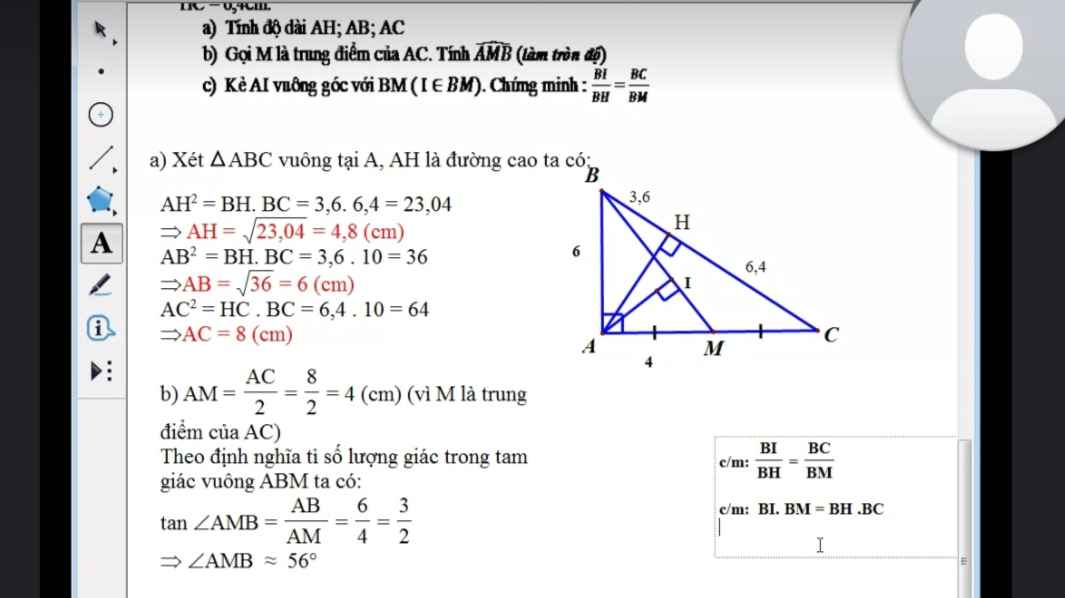
c, Áp dụng HTL ta được \(\left\{{}\begin{matrix}BI\cdot BM=AB^2\\BH\cdot BC=AB^2\end{matrix}\right.\Rightarrow BI\cdot BM=BH\cdot BC\)
\(\Rightarrow\dfrac{BI}{BH}=\dfrac{BC}{BM}\)
8 tháng 11 2021
c: Xét ΔABM vuông tại A có AI là đường cao
nên \(BI\cdot BM=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BI\cdot BM=BH\cdot BC\)
hay \(\dfrac{BI}{BH}=\dfrac{BC}{BM}\)
5 tháng 11 2021
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)
\(a,m=0\Leftrightarrow y=3x+2\)
Vì \(3>0\) nên hàm đồng biến
\(b,\text{Thay }x=-1;y=3\\ \Leftrightarrow-m-3+2=3\Leftrightarrow m=-4\\ c,\text{PT giao Ox: }y=0\Leftrightarrow x=-\dfrac{2}{m+3}\Leftrightarrow A\left(-\dfrac{2}{m+3};0\right)\Leftrightarrow OA=\dfrac{2}{\left|m+3\right|}\\ \text{PT giao Oy: }x=0\Leftrightarrow y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\\ \text{Ta có }S_{OAB}=4\\ \Leftrightarrow\dfrac{1}{2}OA\cdot OB=4\Leftrightarrow\dfrac{2}{\left|m+3\right|}\cdot2=8\\ \Leftrightarrow\dfrac{4}{\left|m+3\right|}=8\\ \Leftrightarrow\left|m+3\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
điểm kìa anh ;-;